問題 3
交流回路に関する記述として、不適当なものはどれか
| a | 回路網の任意の接続点において、流入する電流の和と流出する電流の和は等しい。 |
| b |
並列に接続された抵抗器に流れるそれぞれの電流は、各コンダクタンスの値に反比例した大きさ
となる。 |
| c | 交流波形の波形率は、実効値を平均値で除した値である |
| d | 皮相電力は、有効電力の2乗と無効電力の2乗の和の平方根に等しい |
解答
a‥キルヒホッフの第一法則より成り立ちます
キルヒホッフの第1法則
電気回路の任意の分岐点について、そこに流れ込む電流の和は、そこから流れ出る電流の和に等しい。
キルヒホッフの第2法則
電気回路の任意の一回りの閉じた経路について、電位差の和は 0 である。
b‥コンダクタンスは抵抗値の逆数で定義されます。
並列接続では各抵抗に発生する電圧は等しいです。そのため、オームの法則より電流は各抵抗の値と反比例していると言えます。つまり、コンダクタンスの値に比例します。
c‥波形率は、波形率=実効値/平均値 で定義されます
d‥皮相電力、有効電力、無効電力は皮相電力を斜辺とする直角三角形の関係にあります。そのため、皮相電力はピタゴラスの定理より、有効電力の2乗と無効電力の2乗の和の平方根に等しいと言えます。
問題 4
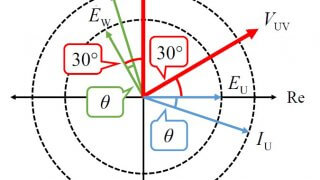
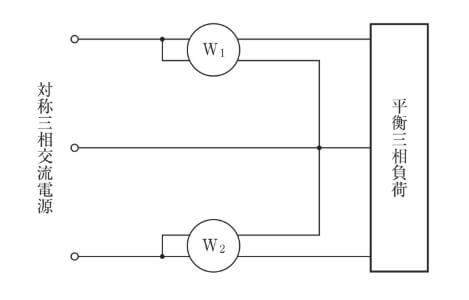
下図に示す平衡三相回路の電力を測定する2電力計法において、線間電圧が \(V\)〔V〕、線電流が \(I\)〔A〕のとき、電力計 \(W_{1}\)、\(W_{2}\)の指示値は、それぞれ\(P_{1}\)〔W〕、\(P_{2}\)〔W〕であった。このとき、負荷の力率を表す式として、正しいものはどれか
| a |
\(\Large{\frac{2VI}{P_{1}+P_{2}}}\)
|
| b | \(\Large{\frac{\sqrt{3}VI}{P_{1}+P_{2}}}\) |
| c |
\(\Large{\frac{P_{1}+P_{2}}{2VI}}\)
|
| d | \(\Large{\frac{P_{1}+P_{2}}{\sqrt{3}VI}}\) |
解答
下記の「ブロンデルの定理と対称平衡三相回路」より「d」が正解