一般的な内圧を受ける内径基準の薄肉構造円筒胴の応力
なお,薄肉構造は直径に比べ厚さが十分小さい場合で,ほとんどのものが該当する。
下図は,内圧p を受ける内径d,肉厚t の薄肉円筒を示している.内圧を受けると円筒の表面の円周方向に\(σ_{θ}\) ,軸方向に\(σ_{z}\) の引張応力が発生する。
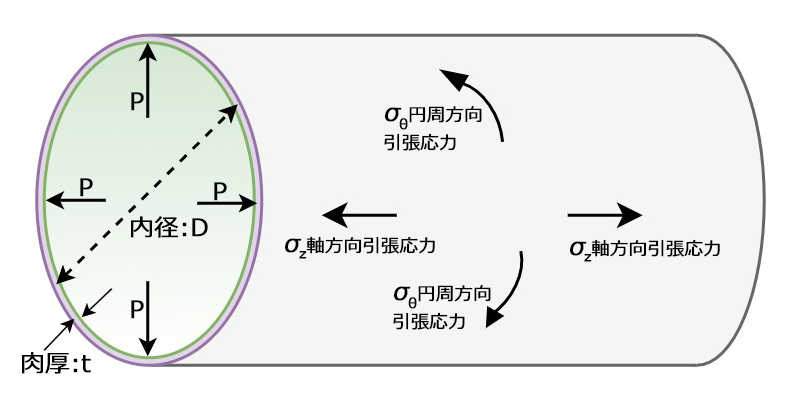
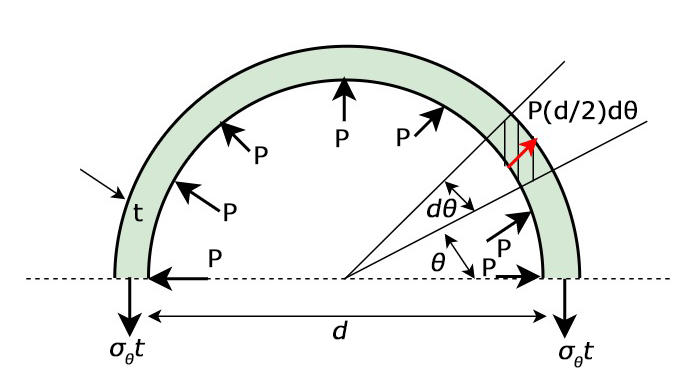
\(σ_{θ}\)は,上図に示した軸方向に単位長さのリングを考えて,直径断面における力の釣り合いから求めるこ
とができる。
\(2\int_{0}^{\frac{π}{2}}P\frac{d}{2}{\sin θ}dθ=2σ_{θ}t\) → \(σ_{θ}=\frac{pd}{2t}\)
\(σ_{z}\) については,端部の円形表面とリング断面について,軸方向の釣り合いから求める。
\(π(\frac{d}{2})^{2}P=2π\frac{d}{2}tσ_{z} → σ_{z}=\frac{pd}{4t}\)
すなわち、円周方向応力\(σ_{θ}\) は軸方向応力\(σ_{z}\) の2 倍となる.したがって,内圧が非常に高くなった場合,破断は\(σ_{θ}\) により軸方向に発生する可能性が高くなる。
さて、\(σ_{θ}=\frac{pd}{2t}\)を使い\(t\)を求める。
\(d\)は板厚の補正項を加えた\(d + m t \),\(σ_{θ}\) は設計温度における材料の許容応力\(σ_{a}\) と溶接継手効率\(η\)の積に置き換えると次式のようになる。m は板厚補正係数である。
\(t=\frac{p(d+mt)}{2σ_{a}η}\) m=1.2とすると
\(t=\frac{pd}{2σ_{a}η-1.2P}\) となり、よく利用される基本式となる。
まとめ
| 内圧を受ける円筒胴の胴板の計算厚さ | |
| 内径を基準とする場合 \(t=\Large{\frac{PD_{i}}{2σ_{a}η-1.2P}}\) 外径を基準とする場合 \(t=\Large{\frac{PD_{o}}{2σ_{a}η+0.8P}}\) | \(t\): 胴板の計算厚さ(㎜) \(P\): 設計圧力(MPa) \(D_{i}\):円筒胴の内径(㎜) \(D_{o}\):円筒胴の外径(㎜) \(σ_{a}\):材料の許容引張応力(\(N/㎜^{2})\) \(η\):長手継手の溶接効率 |
| 内面に圧力を受ける配管の計算厚さ | |
| 管の場合外径を基準とする \(t=\Large{\frac{PD_{o}}{2σ_{a}η+0.8P}}\) | \(t\):管の最小厚さ(㎜) \(P\): 設計圧力(MPa) \(D_{o}\):管の外径(㎜) \(σ_{a}\):材料の許容引張応力(\(N/㎜^{2})\) \(η\):溶接効率 |
冷凍用圧力容器の肉厚等に計算に関する用語の理解
| 最高使用圧力 | |
| 最高使用圧力は許容圧力である \(P=\Large{\frac{2σ_{a}η(t_{a}-α)}{D_{i}+1.2(t_{a}-α)}}\) | \(t\):円筒胴の最小厚さ(㎜) \(P\): 設計圧力(MPa) \(D_{i}\):管の内径(㎜) \(σ_{a}\):材料の許容引張応力(\(N/㎜^{2})\) \(η\):溶接効率 |
| 基準凝縮温度と設計圧力 |
| 冷凍保安規則例示基準の表により求める。 基準凝縮温度以外の時は、最も近い上位の温度に対応する圧力とする。 即ち、最高使用凝縮温度を次の式で求め、算出した温度に最も近い表中の基準凝縮温度に 対応する設計圧力を使用する。 |
