オイラー座屈荷重とは？

 

オイラー座屈荷重とは？

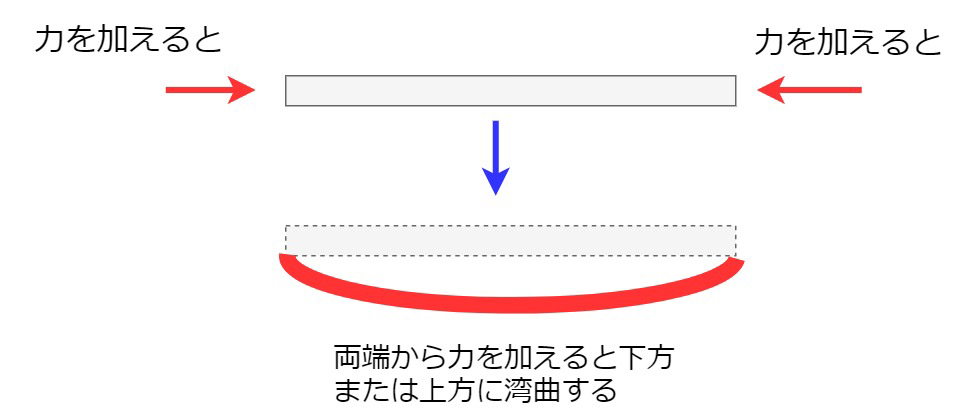
オイラー座屈とは、細長い部材（柱）が圧縮力により横に飛び出し、急激な耐力低下を起こす現象です。プラスチック製のものさしを両手でつまむと、急に「ぐにゃ」となると思います。あの現象が「座屈」です。

オイラー座屈の座屈荷重は、次の式で表されます。
\(P_{cr}=\frac{π^{2}EI}{L_{k}^{2}}\)
\(P_{cr}\)　：　座屈荷重（座屈耐力ともいう）
\(E\)　：　ヤング係数
\(I\)　：　断面二次モーメント
\(L_{k}\)　：　座屈長さ（\(L_{k}=α×L\)で、\(α\)は境界条件に応じた係数、\(L\)は支点間距離）

この式から分かるように、座屈荷重（座屈に抵抗する耐力）は圧縮強度とは無関係です。部材の材質、断面性能、柱の長さ、境界条件で決まります。細長い柱より、太い柱の方が座屈荷重は大きいです。また、木造より鉄骨造の方が、長い柱より短い柱の方が座屈荷重が大きくなります。

オイラー座屈荷重を求める

次の図は。この長柱に圧縮荷重を作用させた場合の状態です。この柱は座屈を起こし、yの変形をおこしているとします。この状態の弾性曲線式は次のように求められます。

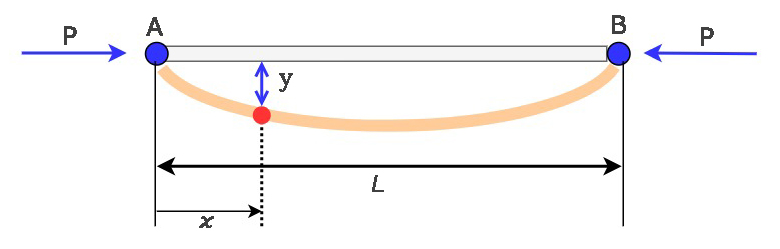
弾性曲線式は以下のように示されます。
\(\frac{d^{2}y}{dx^{2}}=-\frac{M}{EI}\)
曲げモーメントは　\(M=py\)　ですので
\(\frac{d^{2}y}{dx^{2}}=-\frac{py}{EI}\)
ここで　\(\frac{p}{EI}=k^{2}\)　とおくと
\(\frac{d^{2}y}{dx^{2}}=-k^{2}y\)
この微分方程式を解く場合ひとつのテクニックを使います、それは\(y\)を次のように仮定します。
\(y=Ae^{λx}\)
\(y’=Aλe^{λx}\)
\(y”=Aλ^{2}e^{λx}\)
\(Aλ^{2}e^{λx}+k^{2}Ae^{λx}=0\)
\(Ae^{λx}(λ^{2}+k^{2})=0\)

つまり
\(λ^{2}=-k^{2}\)
\(λ=\pm{ki}\)

\(y=Ae^{λx}\) 　にλを代入します。解は2つ存在するので、2つを代入し足し合わせたものがyとなります。
\(y=Ae^{kix}+Be^{-kix}\)

さて、ここで次のオイラーの公式を使います。オイラーの公式とは、eの関数と三角関数をマクローリン展開によって関係づけた式です。
オイラーの公式
\(e^{ix}=\cos{x}+i\sin{x}\)

これを利用すると
\(e^{kix}=\cos{kx}+i\sin{kx}\)
\(e^{-kix}=\cos{kx}-i\sin{kx}\)
となり、\(y\)の式は次のようになります。
$$y=A(\cos{kx}+i\sin{kx})+B(\cos{kx}-i\sin{kx})=(A+B)\cos{kx}+(A-B)\sin{kx}$$

A及びBは定数なので、(A+B),i(A-B)を改めてA、Bと書きなおすと次のようになる。
\(y=A\cos{kx}+B\sin{kx}\)

さて、次の課題は座屈荷重を求めること。まずは境界条件によって定数を求めましょう。境界条件は
\(x=0, y_{1}=0\)
\(x=L, y_{2}=0\)
この２つの境界条件を\(y\)を求める式に代入すると
\(A=0\)
\(B\sin{kL}=0\)
となるが\(B=0\)では方程式が全て0となり意味の無いので、
\(B\neq 0\)　とすると
\(\sin{kL}=0\)
\(kL=n\pi\)　(\(n=1,2.3.・・・(\)

よって、
\(y=B\sin{kx}\)
\(k=\frac{\Large{n\pi}}{L}\)
\(y=B\sin{\frac{\Large{n\pi{x}}}{L}}\)

\(k^{2}=\frac{P}{EI}\)　　\(k=\frac{\Large{n\pi}}{L}\)　だから
\(P=\frac{EI\Large{n^{2}\pi^{2}}}{L^{2}}\)

 

座屈が始まるときの荷重を求めために、nが最小の値である(n=1)のときの、座屈荷重\(P_{cr}\)を決定します。
\(P_{cr}=\frac{\Large{\pi^{2}}EI}{\Large{L^{2}}}\)　　これが座屈荷重です