【問題】R404Aを用いた冷蔵庫用のフインコイル乾式蒸発器が、着霜のない状態で次の仕様および運転条件で運転されている。
ただし、蒸発器出口における冷媒の状態は乾き飽和蒸気とし、冷媒と空気との聞の温度差は算術平均温度差を用い、フインコイル材の熱伝導抵抗は無視できるものとする。
| 【冷凍サイクルの運転条件】 | |
| 有効内外伝熱面積比 | m=20 |
| 冷媒流量 | \(q_{mr}\)=0.11 kg/sec |
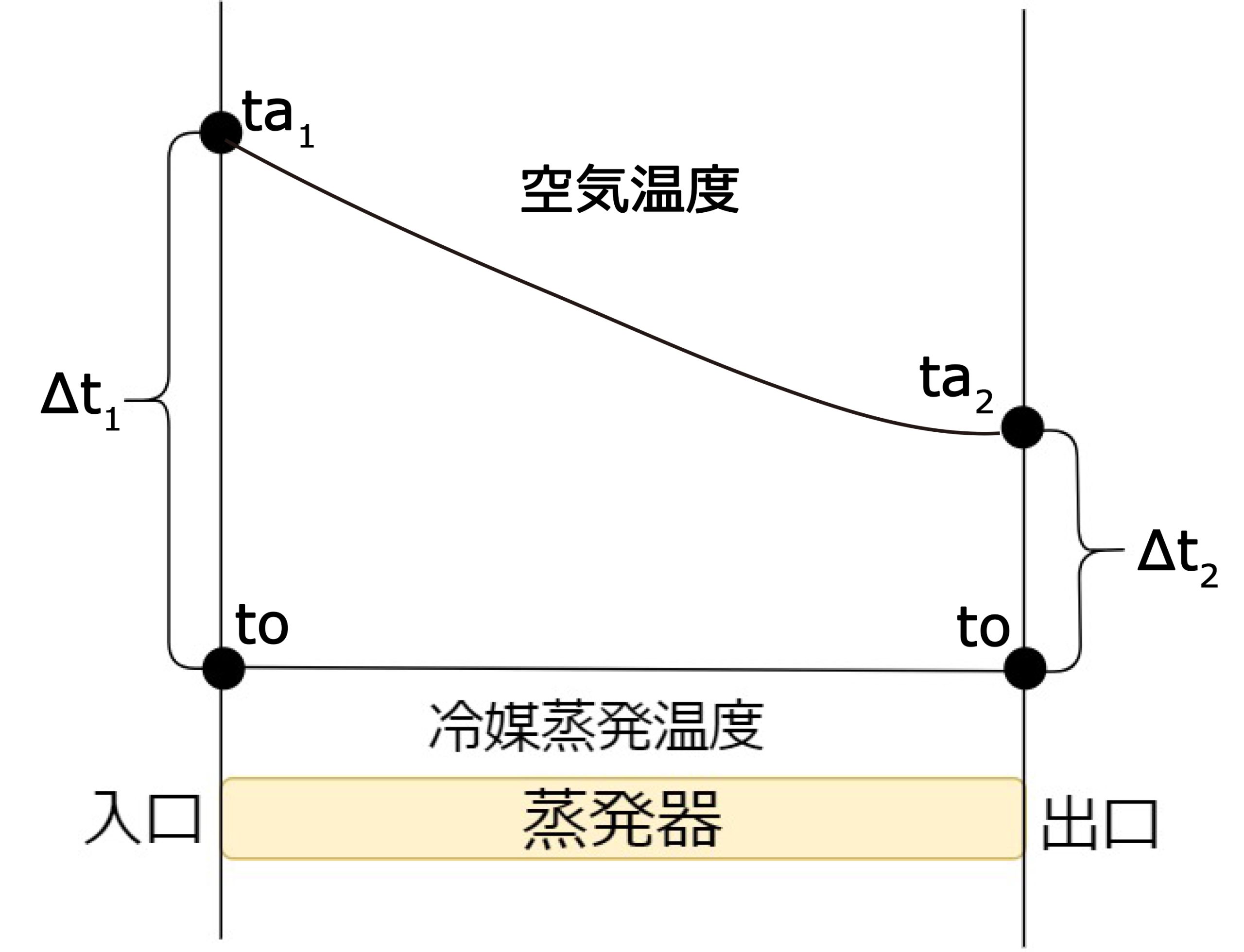
| 冷媒蒸発温度 | \(t_{o}\)=－15℃ |
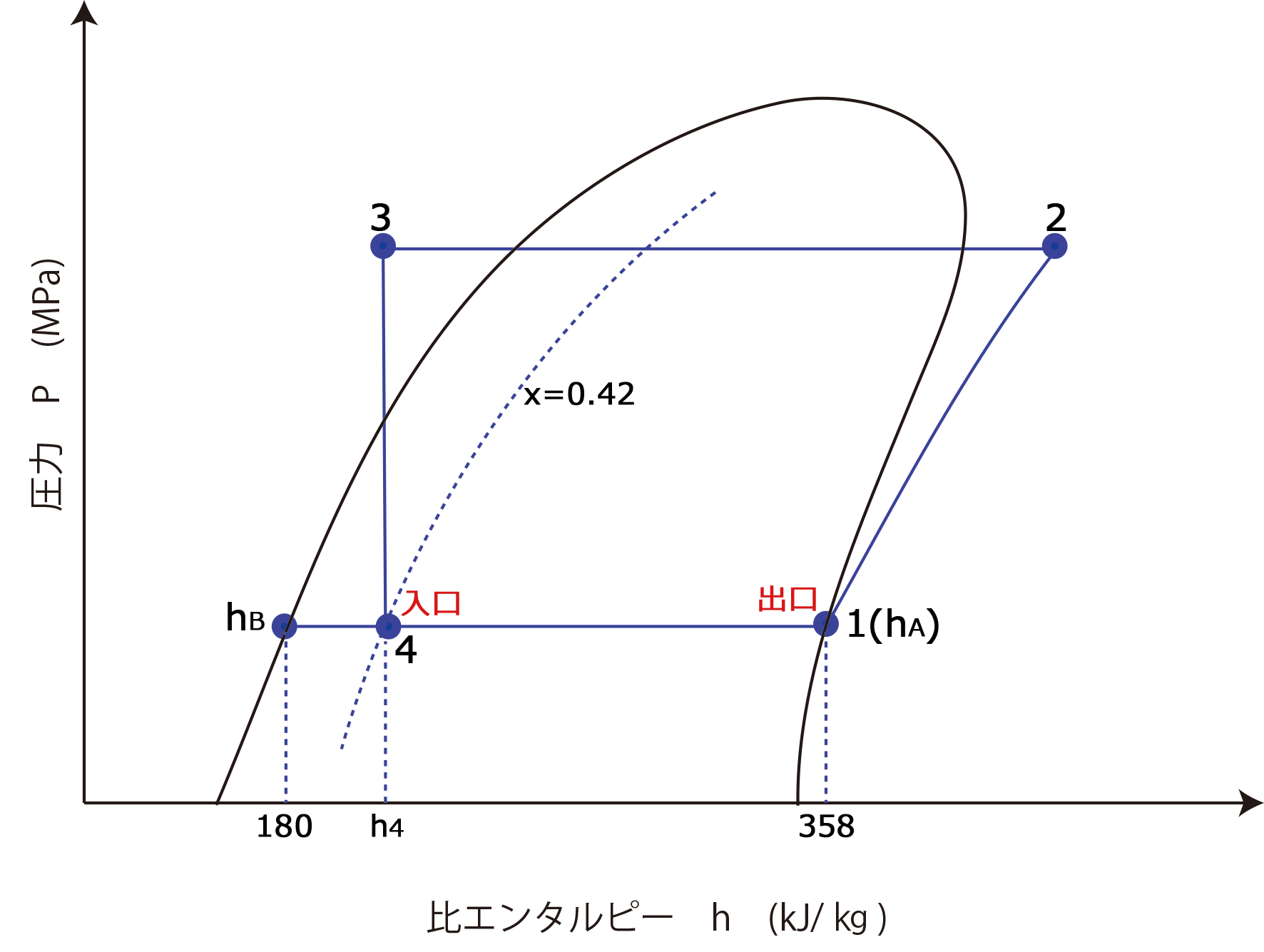
| 蒸発器入口冷媒の乾き度 | \(x\)=0.42 |
| 冷媒蒸発温度における冷媒の比エンタルピー | |
| 飽和液 | \(h_{B}\)＝180 kJ/㎏ |
| 乾き飽和蒸気 | \(h_{A}\)＝358 kJ/㎏ |
| 空気側平均熱通過率 | \(α_{a}\)＝0.045 kW/(m2・K) |
| 冷媒側平均熱通過率 | \(α_{r}\)＝3.6 kW/(m2・K) |
| 入口空気温度 | \(t_{a1}\)＝－5 ℃ |
| 出口空気温度 | \(t_{a2}\)＝－10 ℃ |
１．冷凍能力\(Φ_{o}\)（kW） は？
２．着霜のない状態における蒸発器の外表面積基準の平均熱通過率K [kW/(m2・K)] は？
３．着霜のない状態における蒸発器の空気側伝熱面積A(m2) は？
４．着霜した場合の蒸発器の外表面積基準の平均熱通過率K'[kW/(m2・K)] は？
ただし、霜の熱伝導率\(λ\)は0.18W/(m・K) とし、霜の厚さ\(δ\)は3.0mmとし、それ以外の条件は変わらないものとする。
この問題の解説は次の「上級冷凍受験テキスト」を参考にしました
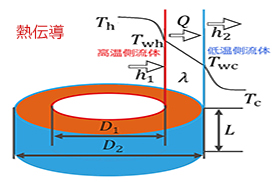
まず、熱通過率に関する基本は別ページ熱伝導についてをご覧ください。よくご存じの方は次に進んでください。
いつものように、p-h線図を次のように書く
１．冷凍能力\(Φ_{o}\)（kW） は？
冷凍能力を求める基本式は
ここで不明なのは\(h_{4}\)であるが、これは乾き度から次のように計算する
変形して
２．着霜のない状態における蒸発器の外表面積基準の平均熱通過率K [kW/(m2・K)] は？
別ページ熱伝導についてに記載の通り
今回の場合は着霜のない状態で、伝熱面積が内外で変わるため次のようになる。
３．着霜のない状態における蒸発器の空気側伝熱面積A(m2) は？
蒸発器入口。出口での温度変化を図に示すと下のようになる、ここで\(Δt_{m}\)は今回は算術平均温度差をとる。
冷凍能力、熱通過率、伝熱面積、温度変化の基本関係式は次の通り、
$$Φ_{o}=K・A・Δt_{m}$$
不明な\(Δt_{m}\)は
４．着霜した場合の蒸発器の外表面積基準の平均熱通過率K'[kW/(m2・K)] は？
ただし、霜の熱伝導率λは0.18W/(m・K) とし、霜の厚さ\(δ\)は3.0mmとし、それ以外の条件は変わらないものとする。
別ページ熱伝導についてに記載の通り
今回は壁を霜と見なして進めると
ここで、単位をm、kWに統一すると
