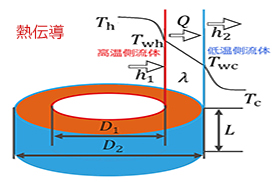
【問題】
以下に示す設計条件でパネル10m2当たりの外気からの侵入熱量\(Φ\)が100Wになるように冷蔵庫パネルを設計した。
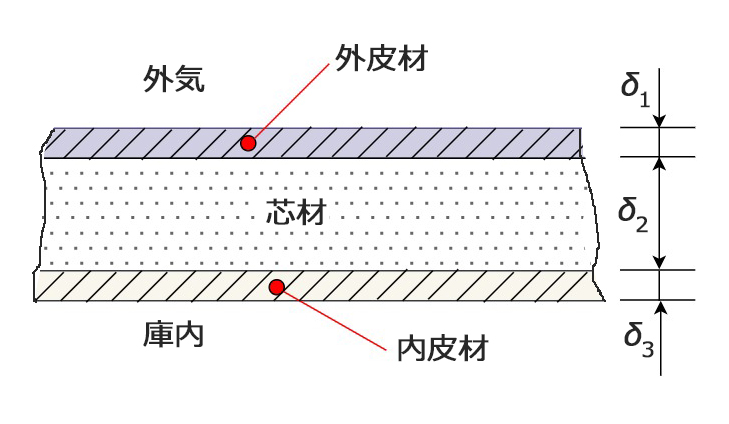
| 【冷凍サイクルの運転条件】 | |
| 外気温度 | \(t_{a}=25℃\) |
| 庫内温度 | \(t_{r}\)=-25℃ |
| パネル外表面(空気側)の熱伝達率 | \(α_{a}\)=10 W/(m2・K) |
| パネル内表面(庫内側)の熱伝達率 | \(α_{r}\)=5 W/(m2・K) |
| パネル外皮材、内皮材の厚さ | \(δ_{1}=δ_{3}\)=0.5㎜ |
| パネル外皮材、内皮材の熱伝導率 | \(λ_{1}=λ_{3}\)=50 W/(m・K) |
| パネル芯材(硬質ポリウレタンフォーム)の熱伝導率 | \(λ_{2}\)=0.030 W/(m・K) |
1.パネルの外表面温度\(tw_{1}\) (℃) は?
2.芯材の厚さ\(δ_{2}\) (mm) は?
3. 外気温\(t_{a}\)が30℃、パネル外表面の熱伝達率\(α_{a}\)が20W/(m2・K)、パネル芯材の厚さが180mmにそれぞれなった場合のパネル10m2当たりの外気からの侵入熱量\(Φ\) (W) は?
この問題の解説は次の「上級冷凍受験テキスト」を参考にしました
【解答】
1.パネルの外表面温度\(tw_{1}\) (℃) は?
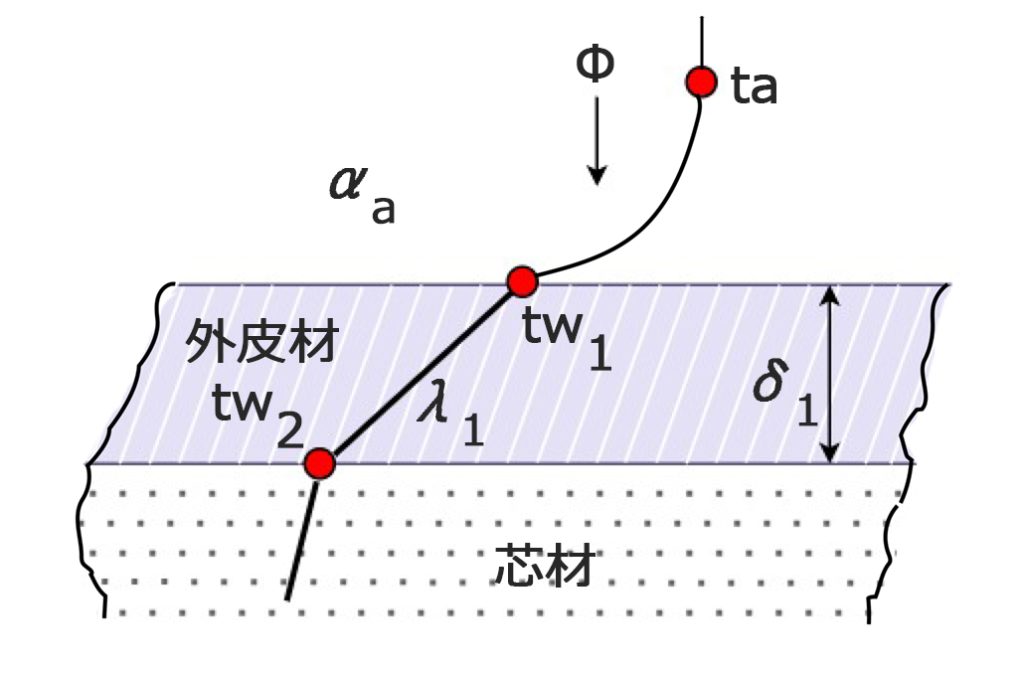
外表面と芯材での構造と温度変化を改めて下図にする
$$Φ=α_{a}・A・(ta-tw_{1})$$ 変形すると
$$tw_{1}=ta-\frac{Φ}{α_{a}・A}=25-\frac{100}{10×10}=24 [℃]$$
2.芯材の厚さ\(δ_{2}\) (mm) は?
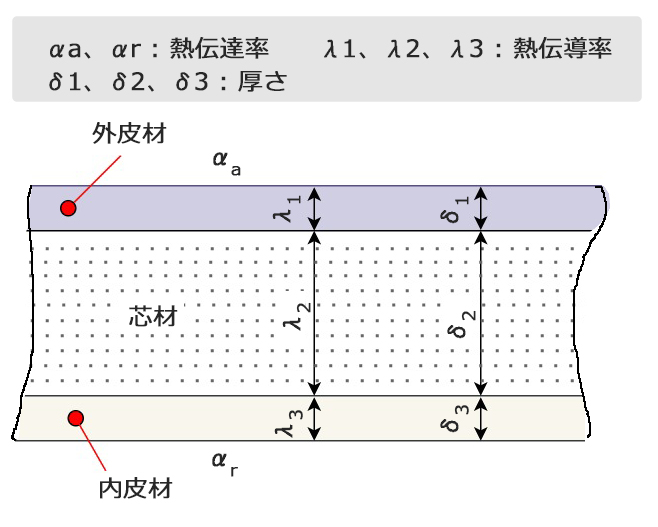
問題図に熱伝導率と熱伝達率を含めて改めて図にすると
次の熱通過率基本式を利用する \(K=\frac{1}{\frac{1}{h_{1}}+\frac{δ}{λ}+\frac{1}{h_{2}}}\)
今回は三層からなるので
$$K=\frac{1}{\frac{1}{α_{a}}+\frac{δ_{1}}{λ_{1}}+\frac{δ_{2}}{λ_{2}}+\frac{δ_{3}}{λ_{3}}+\frac{1}{α_{r}}}$$
$$δ_{2}=λ_{2}×(\frac{1}{K}-\frac{1}{α_{a}}-\frac{δ_{1}}{λ_{1}}-\frac{δ_{3}}{λ_{3}}-\frac{1}{α_{r}})$$
Kはまた、次のように表される
$$Φ=K・A・Δt$$
$$Φ=K・A・(t_{a}-t_{r})$$ $$K=\frac{Φ}{A・(t_{a}-t_{r})}=\frac{100}{10×50}=0.2$$
数値を代入すると
$$δ_{2}=0.030×(\frac{1}{0.2}-\frac{1}{10}-\frac{0.5×10^{-3}}{50}-\frac{0.5×10^{-3}}{50}-\frac{1}{5})$$
$$=0.140999(m)≒141(mm)$$
3. 外気温度taが30℃、パネル外表面の熱伝達率\(α_{a}\)が20W/(m2・K)、パネル芯材の厚さが180mmにそれぞれなった場合のパネル10m2当たりの外気からの侵入熱量\(Φ (W)\) は?
まずKの値を求めます
$$K=\frac{1}{\frac{1}{α_{a}}+\frac{δ_{1}}{λ_{1}}+\frac{δ_{2}}{λ_{2}}+\frac{δ_{3}}{λ_{3}}+\frac{1}{α_{r}}}$$
$$=\frac{1}{\frac{1}{20}+\frac{0.0005}{50}+\frac{0.18}{0.03}+\frac{0.0005}{50}+\frac{1}{5}}$$
$$=0.15999≒0.16 [W/m^{2}・K]$$
ここで \(Φ=K・A・Δ_{t}\) を使うと
$$Φ=K・A・Δ_{t}=K・A・(t_{a}-t_{r})=0.16×10×(30-(-25))=88 [W]$$