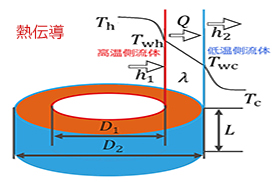
【問題】乾式蒸発器を使用した冷蔵庫の冷却に液ポンプを用いる装置の略図と運転条件を以下に示す。
ただし、冷媒と空気との間の温度差は算術平均温度差を用い、蒸発器、配管における圧力損失による冷媒の温度変化はなく、蒸発器の伝熱管の熱抵抗は無視できるものとする。
| 【運転条件】 | |
| 冷却負荷 | \(Φ\)=100 kW |
| 蒸発器の条件 | |
| 蒸発温度 | \(t_{0}\)=－33 ℃ |
| 入口空気温度 | \(t_{a1}\)=－21 ℃ |
| 出口空気温度 | \(t_{a2}\)=－25 ℃ |
| 有効内外伝熱面積比 | m=20 |
| 空気側熱伝達率 | \(α_{a}\)=0.05 kW/(m2・K) |
| 冷媒側熱伝達率 | \(α_{r}\)=1.0 kW/(m2・K) |
| 霜の厚み | \(δ\)=0.002 m |
| 霜の熱伝導率 | \(λ\)=0.0002 kW/(m2・K) |
| 外気に触れる配管の条件 | |
| 外気側の熱伝達率 | \(α_{o}\)=0.01 kW/(m2・K) |
| 断熱材外径 | \(D\)=0.1 m |
| 断熱材外表面温度 | \(t_{1}\)=27 ℃ |
| 外気からの侵入熱量 | \(Φ_{1}\)=3.0 kW |
| 総配管長（往復） | \(2L\)=124 m |
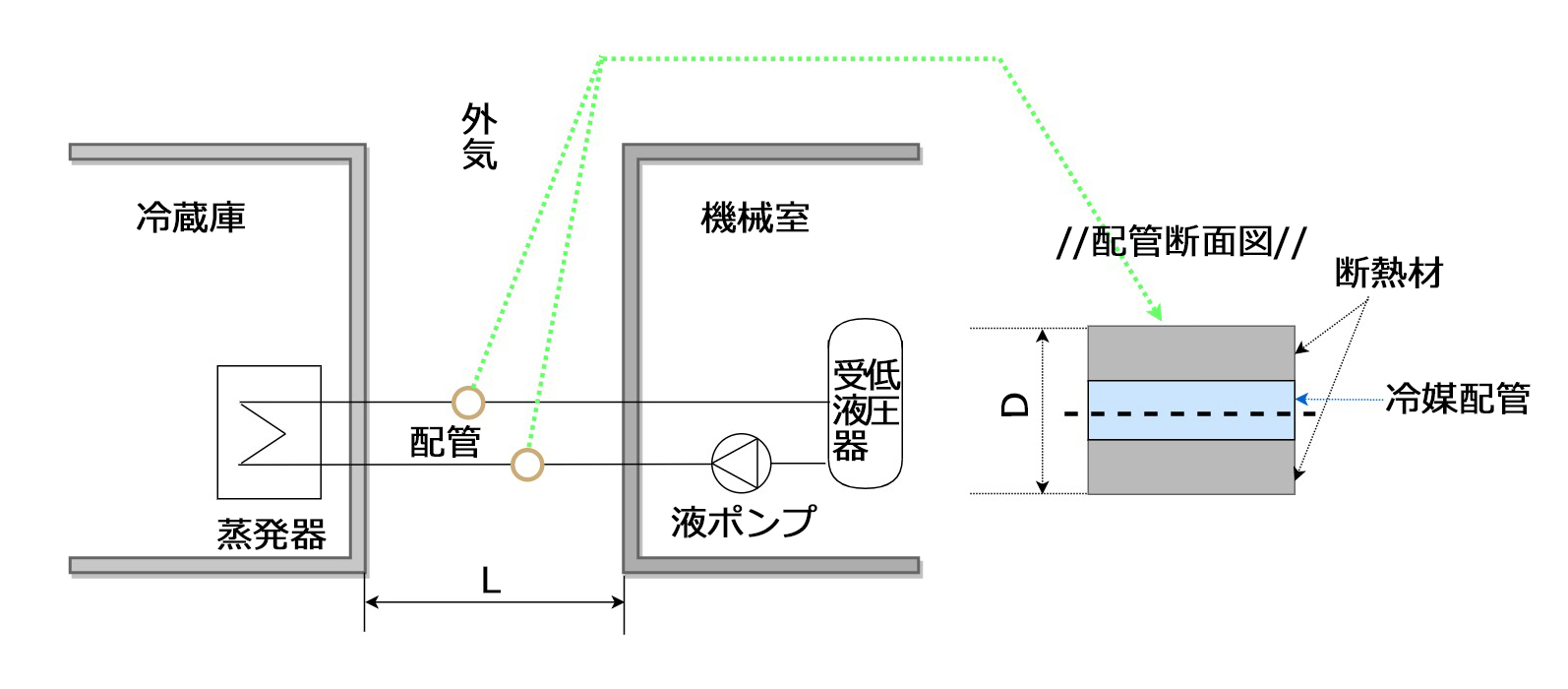
１．蒸発器の外表面基準の平均熱通過率\(K_{o}\)［kW/(m2・K)］ は？
２．蒸発器の外表面伝熱面積\(A\)（m2）は？
３．外気温度\(t_{2}\)（℃） は？
４．外気温度\(t_{2}\)が38℃になった場合の外気から配管への侵入熱量\(Φ_{2}\)（kW） は？
この問題の解説は次の「上級冷凍受験テキスト」を参考にしました
１．蒸発器の外表面基準の平均熱通過率\(K_{o}\)［kW/(m2・K)］ は？
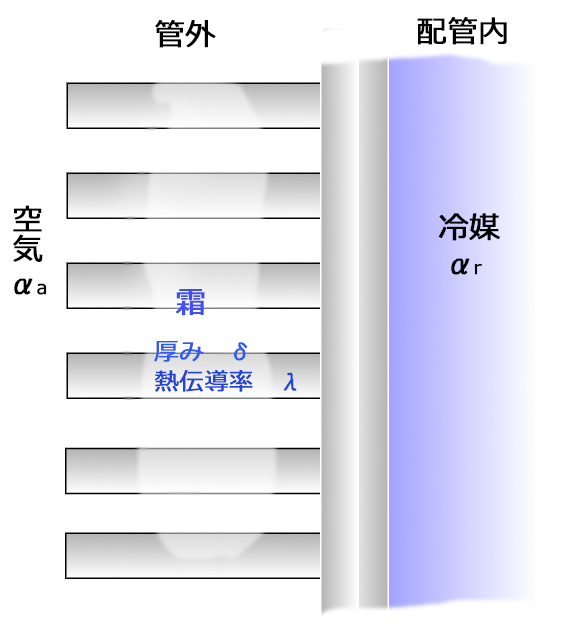
まず、蒸発器付近を図に表すと
熱通過率\(K\)の基本式より（\(m=\frac{外側伝熱面積}{内側伝熱面積}\)、\(δ\)：霜の厚み、\(λ\)：霜の熱伝達率）
今回の場合は
２．蒸発器の外表面伝熱面積\(A\)（m2）は？
蒸発器の冷却負荷は\(Φ\)、前問より平均熱通過率\(K_{o}=0.02\)、蒸発温度と空気入口温度差及び出口温度差を算術平均温度差\(Δt_{m}\)、外表面伝熱面積\(A\)とすれば、次のような関係になる。
\(Φ=K_{o}・A・Δt_{m}\) (Ａ式)
ここで、\(Δt_{a1}=t_{a1}-t_{0} 、 Δt_{a2}=t_{a2}-t_{0}\)だから\(Δt_{m}\)を求める
(Ａ式)を変形して
３．外気温度\(t_{2}\)（℃） は？
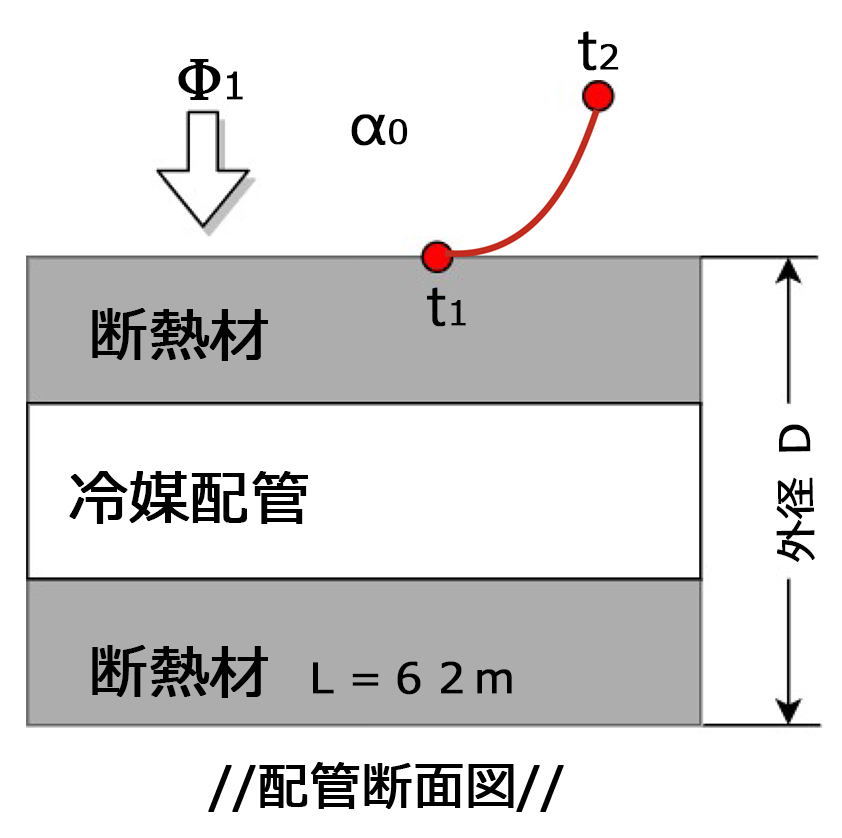
配管断面図を別に下図のように示す
侵入熱量、熱伝達率、伝熱面積、温度変化の関係式は、今回の場合
$$Φ_{1}=α_{0}・A・(t_{2}-t_{1})$$
\(∴ t_{2}=Φ_{1}・\frac{1}{α_{0}・A}+t_{1}\) (Ｂ式)
ここで、伝熱面積\(A\)は
$$A=2・π・\frac{D}{2}・(2L)=2・π・D・L=38.936$$
(Ｂ式)に代入すると
４．外気温度\(t_{2}\)が38℃になった場合の外気から配管への侵入熱量\(Φ_{2}\)（kW） は？
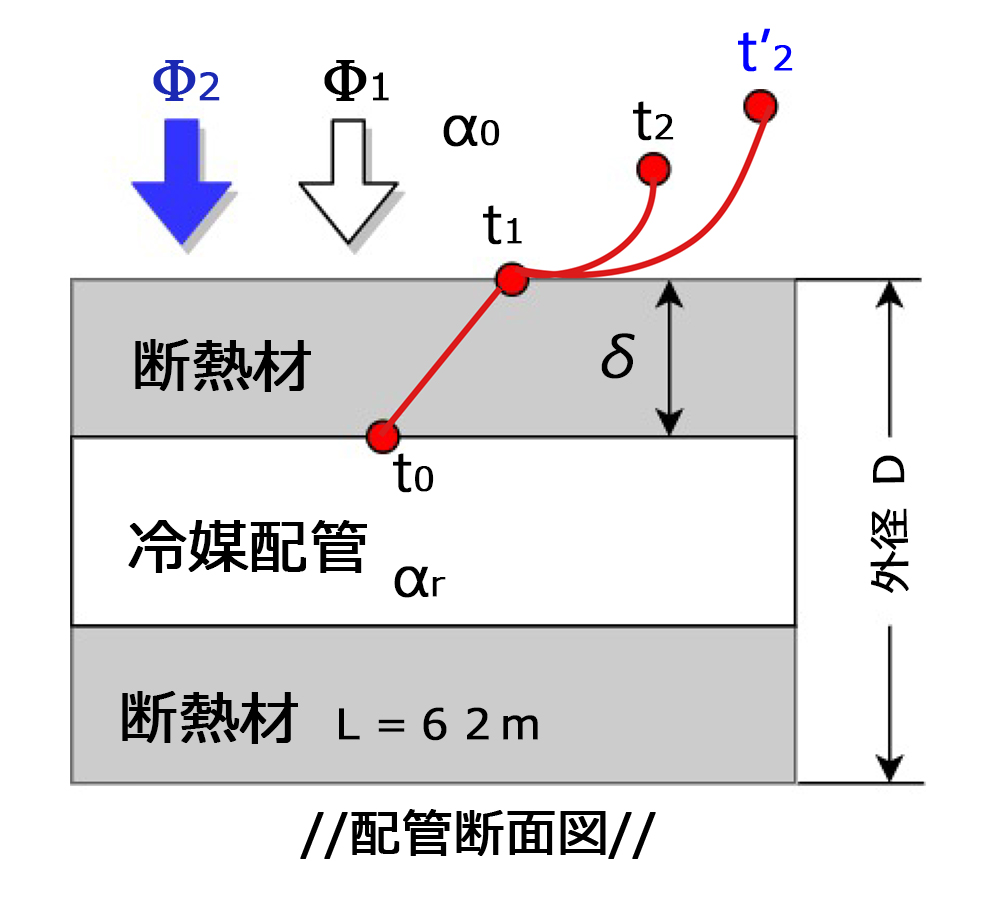
上の配管断面図に\(t_{2}\)が38℃になった時を\(t’_{2}\)として、温度変化を図に書き加えると
とすると次の基本式が成り立つ
$$Φ_{1}=K・A・(t_{2}-t_{0})$$
$$Φ_{2}=K・A・(t’_{2}-t_{0})$$
