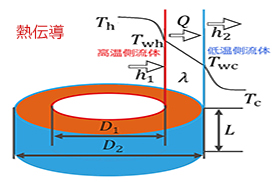
【問題】下図のような材料の組み合わせで、単位面積あたりの侵入熱量\(Φ\)が20 W/m2の冷凍庫パネルを設計したい。
| 【設計条件】 | |
| 外気温度 \(t_{a}\)=32℃、庫内温度\(t_{r}\)=－25℃のとき | |
| パネル外表面の熱伝達率 | \(α_{a}\)=20 W/ (m2・K) |
| パネル内表面の熱伝達率 | \(α_{r}\)=7 W/ (m2・K) |
| 外皮材（カラー鋼板）の厚さ | \(δ_{1}\)=0.5 ㎜ |
| 内皮材（カラー鋼板）の厚さ | \(δ_{3}\)=0.5 ㎜ |
| 外皮材（カラー鋼板）の熱伝導率 | \(λ_{1}\)=40 W/(m・K) |
| 芯材（硬質ポリウレタンフォーム）の熱伝導率 | \(λ_{2}\)=0.03 W/(m・K) |
| 内皮材（カラー鋼板）の熱伝導率 | \(λ_{3}\)=40 W/(m・K) |
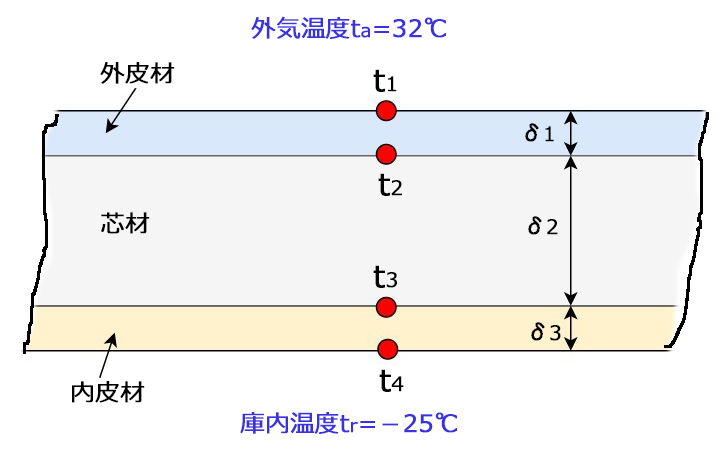
１．パネルの熱通過率K［W/(m2・K)］ は？
２．芯材の外皮材と接する温度\(t_{2}\)（℃）は？
３．芯材の厚さ\(δ_{2}\)（mm） は？
この問題の解説は次の「上級冷凍受験テキスト」を参考にしました
１．パネルの熱通過率K［W/(m2・K)］ は？
まず、伝熱量\(Φ\)、熱通過率\(K\)、伝熱面積\(A\)、温度差\(Δt\)の関係基本式は
\(Φ=K・A・Δt\) だが、問題の\(Φ\)は単位面積なので、\(A=1\)とすると
\(Φ=K・Δt\) となるので
$$K=\frac{Φ}{Δt}=\frac{20}{32-(-25)}=0.35 (W/m^{2}・K)$$
２．芯材の外皮材と接する温度\(t_{2}\)（℃）は？
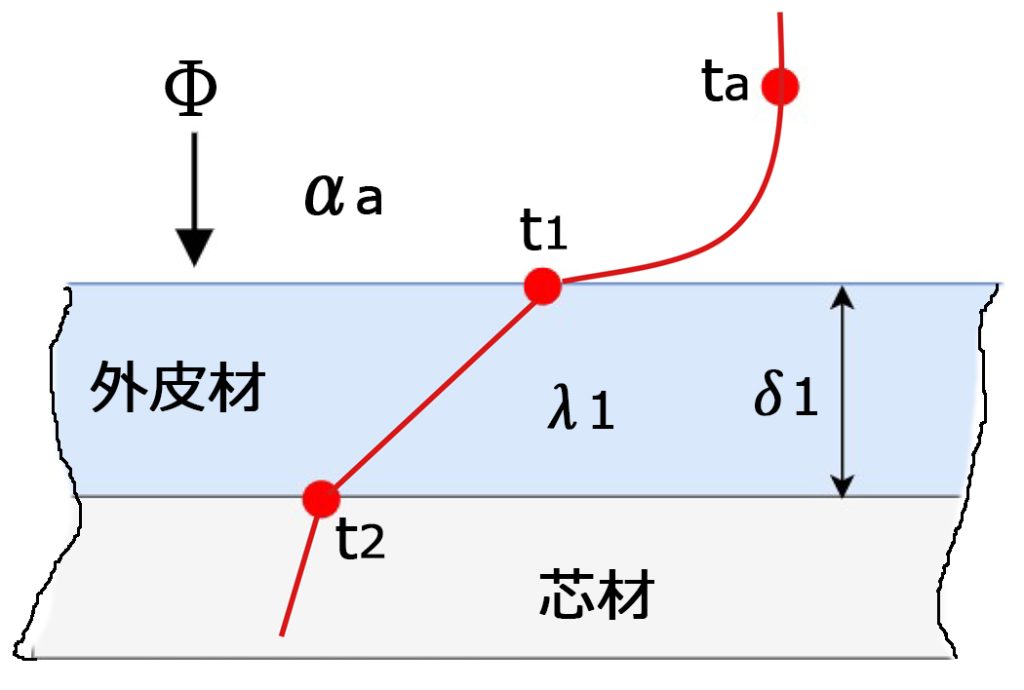
\(Φ=α_{a}・A・(t_{a}-t_{1})\) となるが前問同様\(A=1\)とすると
$$t_{1}=t_{a}-\frac{Φ}{α_{a}}=32-\frac{20}{20}=31$$
また、\(Φ=\frac{λ_{1}}{δ_{1}}・A・(t_{1}-t_{2})\) で変形すると(ただし、\(A=1\))
$$t_{1}=t_{a}-\frac{Φ}{α_{a}}=32-\frac{20}{20}=31$$
また、\(Φ=\frac{λ_{1}}{δ_{1}}・A・(t_{1}-t_{2})\) で変形すると(ただし、\(A=1\))
$$t_{2}=t_{1}-\frac{Φ・δ_{1}・10^{-3}}{λ_{1}}=31-\frac{20・0.5・10^{-3}}{40}=30.99975 ℃$$
３．芯材の厚さ\(δ_{2}\)（mm） は？
詳細を下図のように示す
外気から冷蔵庫内への熱通過率\(K\)は次のようになる
$$K=\frac{1}{\frac{1}{α_{a}}+\frac{δ_{1}}{λ_{1}}+\frac{δ_{2}}{λ_{2}}+\frac{δ_{3}}{λ_{3}}+\frac{1}{α_{r}}}$$
変形すると
$$δ_{2}=λ_{2}・(\frac{1}{K}-\frac{1}{α_{a}}-\frac{δ_{1}}{λ_{1}}-\frac{δ_{3}}{λ_{3}}-\frac{1}{α_{r}})$$
数値を代入すると（ここで、\(\frac{δ_{1}}{λ_{1}}\)と\(\frac{δ_{3}}{λ_{3}}）\)は無視できるほど小さいので計算から除外する）
$$δ_{2}=λ_{2}・(\frac{1}{K}-\frac{1}{α_{a}}-\frac{1}{α_{r}})=0.03・(\frac{1}{0.35}-\frac{1}{20}-\frac{1}{7})=0.0799 m≒80 mm$$
