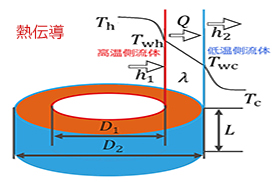
【問題】R410A冷凍装置における空冷凝縮器が次の仕様および運転条件で運転されている。
ただし、冷媒凝縮温度と冷却空気温度との間の温度差は算術的平均温度差を用い、冷却管材の熱伝導抵抗と冷却管の汚れの影響は無視できるものとする。
| 【仕様及び運転条件】 | |
| 凝縮負荷 | \(Φ_{K}=130 kW\) |
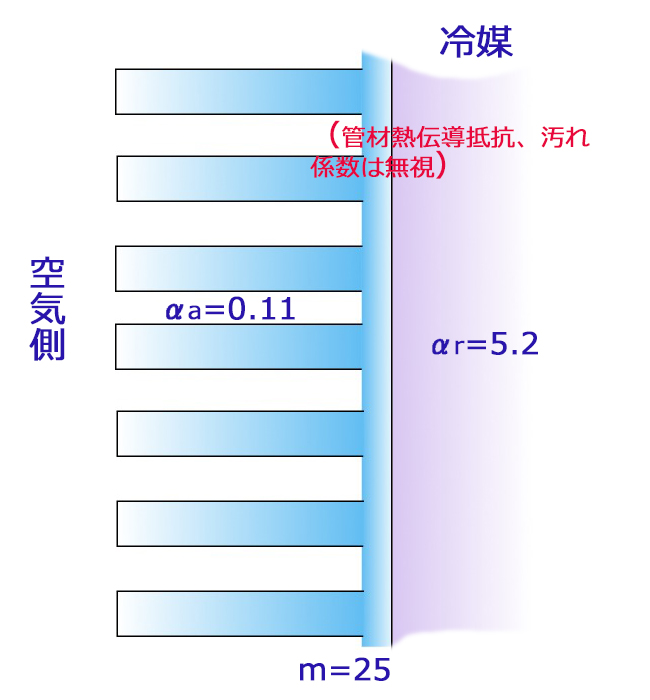
| 有効内外伝熱面積比 | m=25 |
| 凝縮器の空気側伝熱面積 | \(A_{a}=180 m^{2}\) |
| 空気側平均熱伝達率 | \(α_{a}=0.11 kW/(m^{2}・K)\) |
| 冷媒側平均熱伝達率 | \(α_{r}=5.2 kW/(m^{2}・K)\) |
| 送風機の送風量 | \(q_{va}=583 m^{3}/min\) |
| 凝縮器の入口空気温度 | \(t_{a1}\)=32.0 ℃ |
| 冷却空気の比熱 | \(C_{a}=1.01 kJ/(kg・K)\) |
| 冷却空気の密度 | \(ρ_{a}=1.18 kg/m^{3}\) |
１．凝縮器の出口空気温度\(t_{a2}\)（℃） は？
２．凝縮器の外表面の面積を基準とする平均熱通過率\(K［kW/(m^{2}・K)］\)を小数点以下3桁まで求めよ。
３．冷媒凝縮温度と冷却空気温度との算術的平均温度差\(ΔT_{m}（K）\) は？
４．冷媒凝縮温度\(t_{k}\)（℃） は？
この問題の解説は次の「上級冷凍受験テキスト」を参考にしました
まず、整理するために、下図を記しておく
１．凝縮器の出口空気温度\(t_{a2}\)（℃） は？
凝縮負荷\(Φ_{K}\)、冷却空気の比熱\(C_{a}\)、冷却空気の密度|(Ρ_{a}\)、送風量\(q_{va}\)、凝縮器入口出口の温度差\(Δt_{a}\)の関係式は
$$Φ_{K}=C_{a}・q_{va}・Ρ_{a}・Δt_{a}$$
\(Δt_{a}=t_{a2}-t_{a1}\)だから
$$Φ_{K}=C_{a}・q_{va}・Ρ_{a}・(t_{a2}-t_{a1})$$
変形すると
数値を代入すると
２．凝縮器の外表面の面積を基準とする平均熱通過率\(K［kW/(m^{2}・K)］\)を小数点以下3桁まで求めよ。
上の図より、熱通過率\(K\)は次の通り
３．冷媒凝縮温度と冷却空気温度との算術的平均温度差\(ΔT_{m}（K）\) は？
凝縮負荷\(Φ_{K}\)、熱通過率\(K\)、伝熱面積\(A_{a}\)、平均温度差\(ΔT_{m}\)の関係式は次の通り
$$Φ_{K}=K・A_{a}・ΔT_{m}$$
変形すると
４．冷媒凝縮温度\(t_{k}\)（℃） は？
算術的平均温度差\(ΔT_{m}\)は次の通り
変形すると
