【問題】
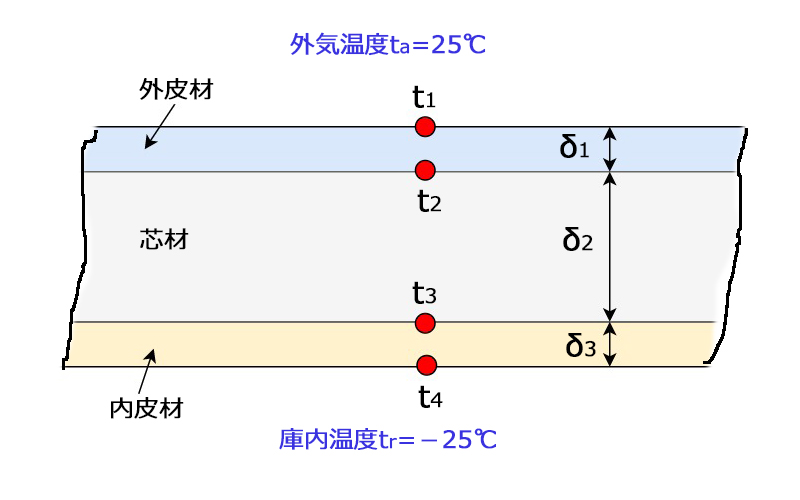
下図のような材料の組み合わせで、単位面積あたりの侵入熱量\(Φ\)が20 W/m2の冷凍庫パネルを設計したい。
| 【設計条件】 | |
| 外気温度 | \(t_{a}\)=25℃ |
| 庫内温度 | \(t_{r}\)=-25℃ |
| パネル外表面(外気側)の熱伝達率 | \(α_{a}\)=10.0 W/ (m2・K) |
| パネル内表面(庫内側)の熱伝達率 | \(α_{r}\)=5.0 W/ (m2・K) |
| パネル外皮材の厚さ及び熱伝導率 | \(δ_{1}\)=0.5 ㎜、\(λ_{1}\)=50 W/(m・K) |
| パネル芯材の厚さ及び熱伝導率 | \(δ_{2}\)=150.0 ㎜、\(λ_{2}\)=0.03 W/(m・K) |
| パネル内皮材の厚さ及び熱伝導率 | \(δ_{3}\)=5.0 ㎜、\(λ_{3}\)=2.0 W/(m・K) |
1. 外気から庫内までの熱通過率K[W/(m2・K)]および1m2当たりの外気からの伝熱量Φ(W)をそれぞれ求めよ
2.芯材のパネル内皮材の間の温度t3(℃)を求めよ
3.パネル芯材に水分が侵入すると、1m2当たりの外気からの伝熱量が18Wとなることがわかった。この際のパネル芯材の見かけの熱伝導率\(λ’_{2}\)[W/(m・K)]を求めよ
この問題の解説は次の「上級冷凍受験テキスト」を参考にしました
【解答】
1.外気から庫内までの熱通過率K[W/(m2・K)]および1m2当たりの外気からの伝熱量Φ(W)をそれぞれ求めよ
次の「熱伝導について」の「熱通過率」の項を参考にすると
熱通過率Kは
\(K=\Large{\frac{1}{\frac{1}{α_{a}}+\frac{δ_{1}}{λ_{1}}+\frac{δ_{2}}{λ_{2}}+\frac{δ_{3}}{λ_{3}}+\frac{1}{α_{r}}}}\)
ここで、単位をm、Wに統一して上の式に数値を代入すると
\(K=\Large{\frac{1}{\frac{1}{10}+\frac{0.0005}{50}+\frac{0.15}{0.03}+\frac{0.005}{2}+\frac{1}{5}}}\)≒0.189(W/m2・K)
伝熱量\(Φ\)、熱通過率\(K\)、伝熱面積\(A\)、温度差\(Δt\)の関係基本式は
\(Φ=K・A・Δt\) だが、問題の\(Φ\)は単位面積なので、\(A=1\)とすると\(Φ=K・Δt\) となるので
$$Φ={K}{Δt}=0.189・(25-(-25))=9.45≒9.5 (W)$$
2.芯材のパネル内皮材の間の温度t3(℃)を求めよ
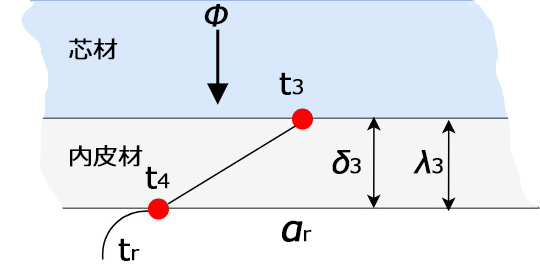
パネル内表面(庫内側)の伝熱量\(Φ\)、熱通過率\(α_{r}\)、伝熱面積\(A\)、温度差\(Δt\)の関係式は
\(Φ=α_{r}・A・Δt\) となり、
\(t_{4}-t_{r}=\Large{\frac{Φ}{α_{r}・A}}\) 式A
また、内皮材の伝熱量\(Φ\)、熱伝導率\(λ_{3}\)、厚さ\(δ_{3}\)、伝熱面積\(A\)、温度差\(Δt\)の関係式は
\(Φ=\Large{\frac{λ_{3}・A・Δt}{δ_{3}}}\) となり
\(t_{3}-t_{4}=\Large{\frac{Φ・δ_{3}}{λ_{3}・A}}\) 式B
式A+式Bは
\(t_{3}-t_{r}=Φ・\Large{(\frac{1}{α_{r}・A}+\frac{δ_{3}}{λ_{3}・A})}\) となる、
単位面積\(A=1\)当たりの伝熱量\(Φ\)は前問解答より9.5だから
\(t_{3}-(-25)=9.5・\Large{(\frac{1}{5.0}+\frac{0.005}{2.0})}\)=1.92375
\(t_{3}=-23.07625≒-23.1\)℃
3.パネル芯材に水分が侵入すると、1m2当たりの外気からの伝熱量が18Wとなることがわかった。この際のパネル芯材の見かけの熱伝導率\(λ’_{2}\)[W/(m・K)]を求めよ
詳細を下図のように示す
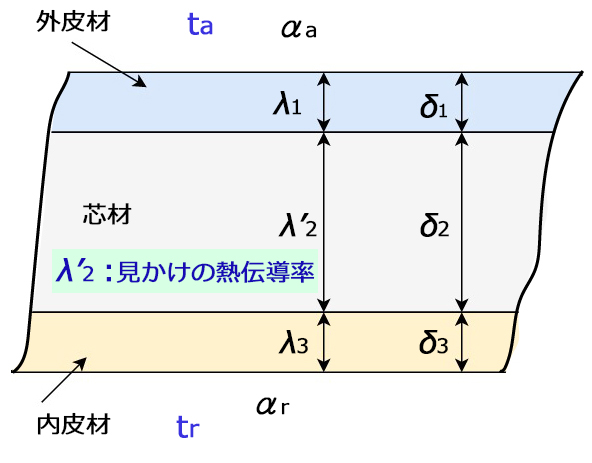
外気から冷蔵庫内への熱通過率\(K’\)、伝熱量\(Φ\)、温度差\(Δt\)の関係式は次のようになる
\(Φ=K’・Δt\)だから
熱通過率K’は \(\Large{K’=\frac{Φ}{Δt}=\frac{Φ}{t_{a}-t_{r}}=\frac{18}{25-(-25)}=\frac{18}{50}=0.36}\)
一般的に熱通過率\(K\)、熱伝達率\(α\)、熱伝導率\(λ\)、厚さ\(δ\)の関係式は次の通り
\(K=\Large{\frac{1}{\frac{1}{α}+\frac{δ}{λ}}}\) となり、今回の場合は
\(K’=\Large{\frac{1}{\frac{1}{α_{a}}+\frac{δ_{1}}{λ_{1}}+\frac{δ_{2}}{λ’_{2}}+\frac{δ_{3}}{λ_{3}}+\frac{1}{α_{r}}}}\)
上記式を変形すると
\(λ’_{2}=\Large{\frac{δ_{2}}{\frac{1}{K’}-\frac{1}{α_{a}}-\frac{δ_{1}}{λ_{1}}-\frac{δ_{3}}{λ_{3}}-\frac{1}{α_{r}}}}\)
数値を代入すると
\(λ’_{2}=\Large{\frac{0.15}{\frac{1}{0.36}-\frac{1}{10}-\frac{0.0005}{50}-\frac{0.005}{2}-\frac{1}{5}}}\)
≒0.06059≒0.061 (W/m・K)