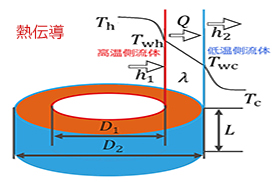
【問題】
以下に示す設計条件で、冷蔵庫パネル外表面での結露を防ぐために、パネル外表面温度ta3が34.5℃以上となるように、冷蔵庫パネルの芯材厚さを決定したい。その場合の最も薄い芯材の厚さを計算式を示して求めよ。さらに、下記の選択肢の中から最も適切な芯材厚さを選択し、その理由を記せ。
| 【設計条件】 | |
| 外気温度 | \(t_{a}\)=35℃ |
| 外気の露点温度 | \(t_{a2}\)=31℃ |
| 庫内温度 | \(t_{r}\)=-25℃ |
| パネル外表面(外気側)の熱伝達率 | \(α_{a}\)=30.0 W/ (m2・K) |
| パネル内表面(庫内側)の熱伝達率 | \(α_{r}\)=5.0 W/ (m2・K) |
| パネル外皮材、内皮材の厚さ | \(δ_{1}\)=\(δ_{3}\)=0.5mm |
| パネル外皮材、内皮材の熱伝導率 | \(λ_{1}\)=\(λ_{3}\)=40 W/(m・K) |
| パネル芯材(硬質ポリウレタンフォーム)の熱伝導率 | \(λ_{2}\)=0.03 W/(m・K) |
[選択肢]
パネル芯材厚さ : 100mm、110mm、120mm、130mm
この問題の解説は次の「上級冷凍受験テキスト」を参考にしました
【解答】
上記問題の設定条件を図に表すと次のようになる
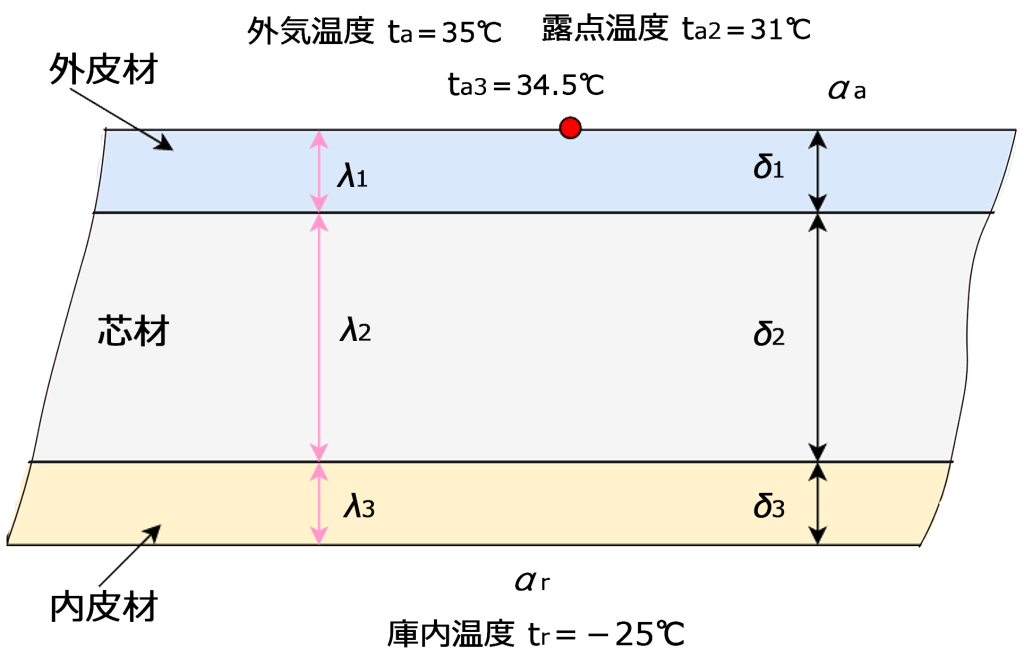
●単位時間あたりの伝熱量Φを求める
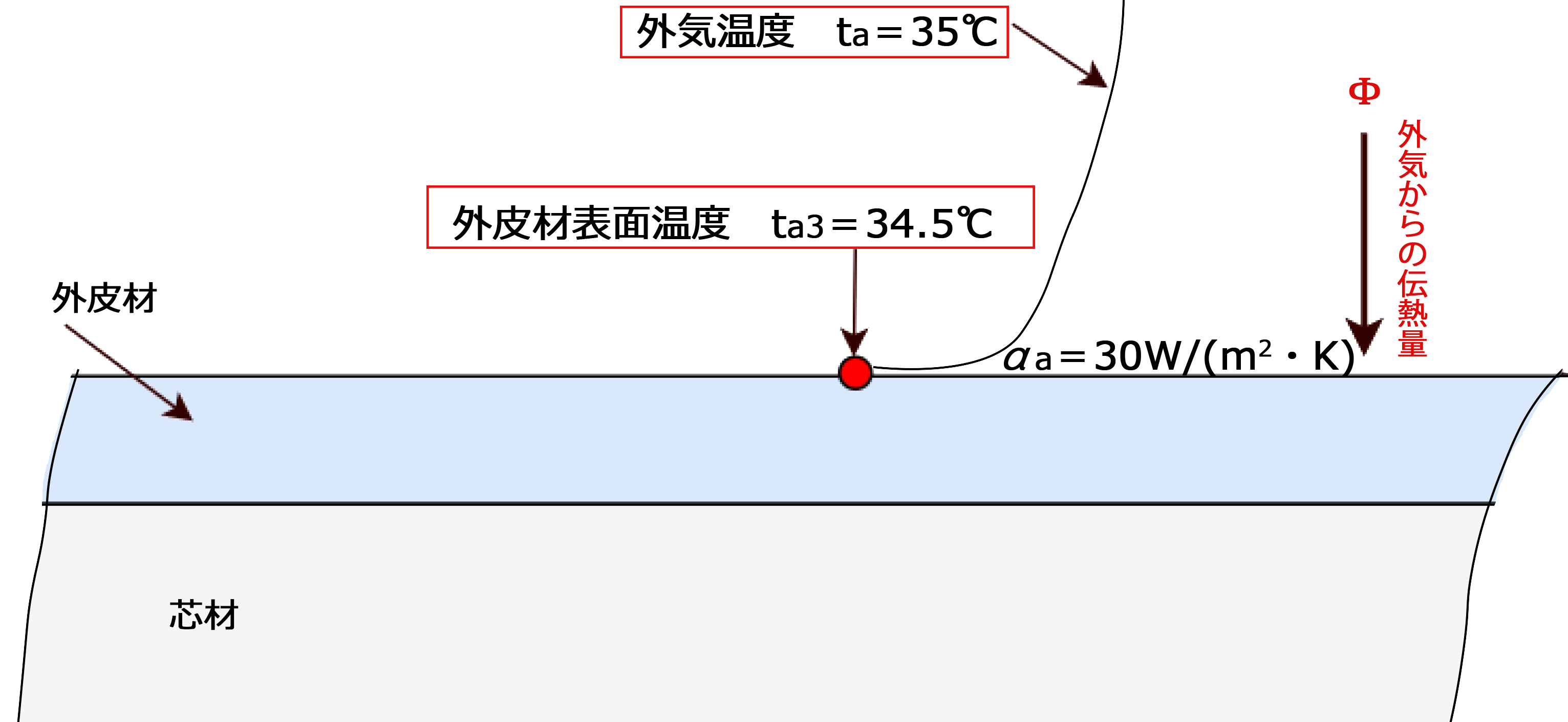
外気からの単位時間あたりの伝熱量Φを求めるため、次のように外気付近を図面化する
単位時間あたりの伝熱量\(Φ\)〔kW〕、外気温\(t_{a}\)、パネル外表面温度\(t_{a3}\)、伝熱面積\(A\)、外気側熱伝達率\(α_{a}\)の関係式(「上級 冷凍受験テキスト」に掲載)は次の通り
| \(\color{red}{t_{a}-t_{a3}}\)=\(\color{red}{Φ\large{\frac{1}{α_{a}A}}}\) |
上式を変形し、単位面積当たりの\(Φ\)を求める[\(A=1\)また単位はW]
\(Φ\)=\(α_{a}A(t_{a}-t_{a3})\)=\(30×(35.0-34.5)\)=15
●単位面積当たりの熱通過率Kを求める(A=1)
| \(\color{red}{Φ}\)=\(\color{red}{KA(t_{a}-t_{r})}\) |
上式を変形して
\(K\)=\(\frac{\large{Φ}}{\Large{t_{a}-t_{r}}}\)=\(\frac{\large{15}}{\large{35-(-25)}}\)=0.25
●最後に芯材厚さ\(δ_{2}\)を求める
| 熱通過率基本公式 \(\color{red}{\large{\frac{1}{K}}}\)=\(\color{red}{\Large{\frac{1}{α_{a}}+\frac{δ_{1}}{λ_{1}}+\frac{δ_{2}}{λ_{2}}+\frac{δ_{3}}{λ_{3}}+\frac{1}{α_{r}}}}\) |
上式を変形して\(δ_{2}\) を求める
\(\large{\frac{δ_{2}}{λ_{2}}}\)=\(\large{\frac{1}{K}-\frac{1}{α_{a}}-\frac{δ_{1}}{λ_{1}}-\frac{δ_{3}}{λ_{3}}-\frac{1}{α_{r}}}\)
\(δ_{2}\)=\(λ_{2}×(\large{\frac{1}{K}-\frac{1}{α_{a}}-\frac{δ_{1}}{λ_{1}}-\frac{δ_{3}}{λ_{3}}-\frac{1}{α_{r}})}\)
数値を代入する
\(δ_{2}\)=\(0.03×(\large{\frac{1}{0.25}-\frac{1}{30}-\frac{0.0005}{40}-\frac{0.0005}{40}-\frac{1}{5})}\)\(≒0.11299m\)
答え 113mmに大きくて小さい120mmが正解