スポンサーリンク
レンツの法則、ファラデーの法則
レンツの法則
コイルを貫く磁束が変化すると、電磁誘導によってコイルに誘導起電力が発生し、その誘導起電力によりコイルに誘導電流が流れます。
このとき発生する誘導起電力は、「誘導電流によってつくられる磁束」が「コイルを貫く磁束の変化」を妨げるような向きに生じます。これをレンツの法則といいます。
磁石をコイルに近づける場合
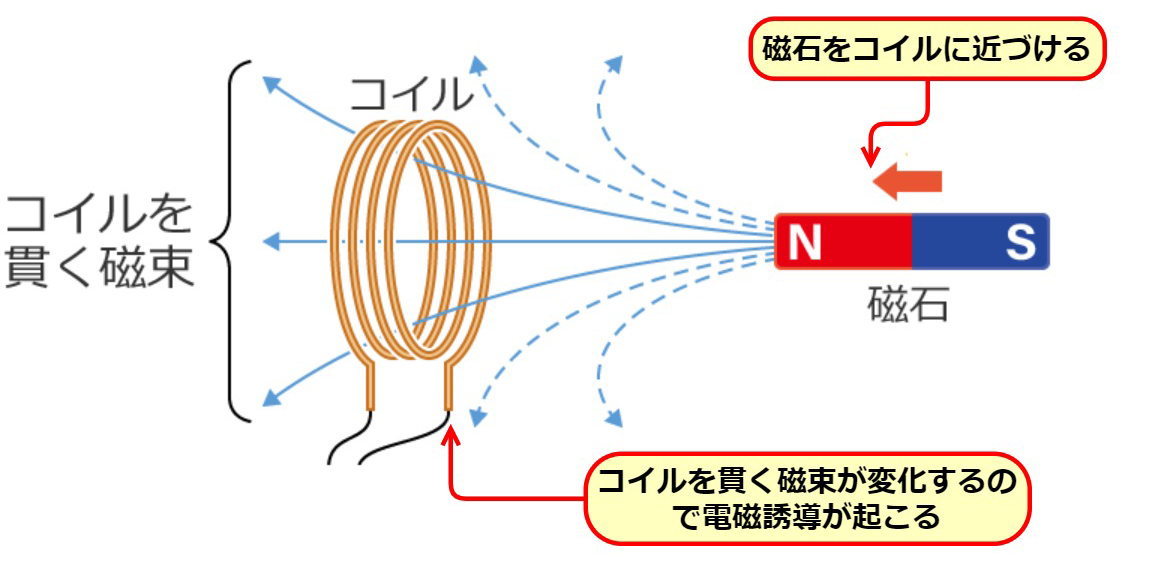
磁石をコイルに近づけます。(磁石をコイルに近づけると、コイルを貫く磁束が変化(増加)するので電磁誘導
が起こります。)
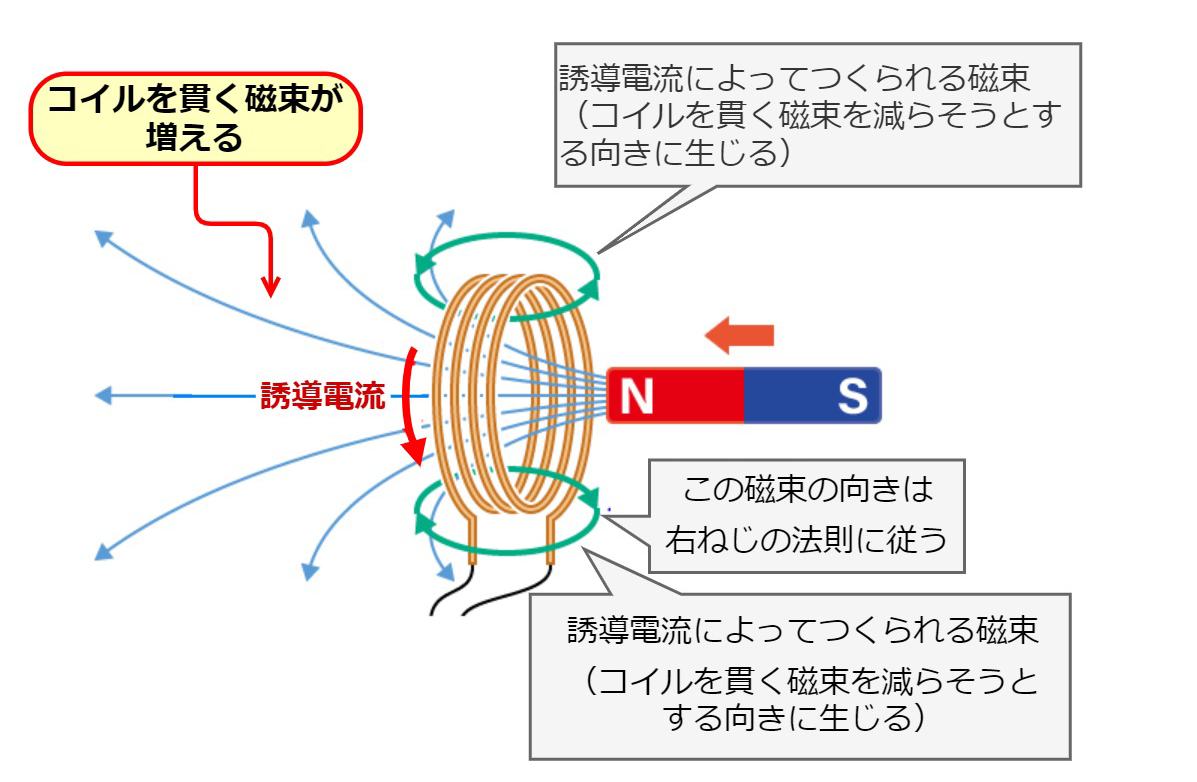
磁石をコイルに近づけるとコイルを貫く磁束が増加するので、誘導電流によってつくられる磁束は、コイルを貫く磁束を減らそうとする向き(コイルを貫く磁束が増加するのを妨げようとする向き)に生じます。
すなわち、左図のような向きの磁束(図中の緑色の磁束)をつくるように誘導電流が流れます。
磁石をコイルから遠ざける場合

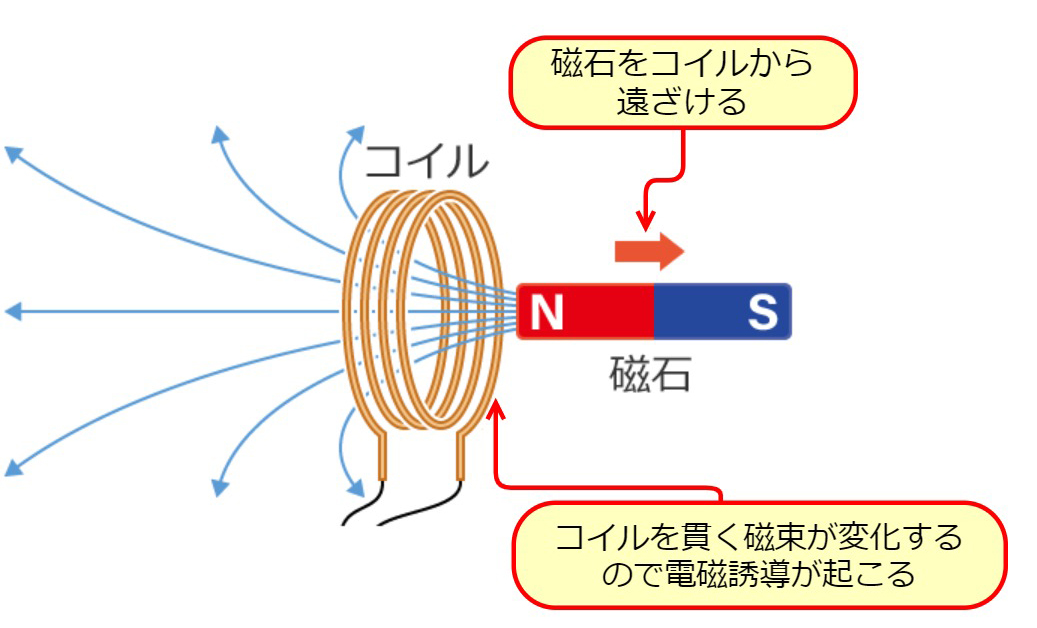
磁石をコイルから遠ざけてみます。(磁石をコイルから遠ざけると、コイルを貫く磁束が変化(減少)するので電磁誘導が起こります。)
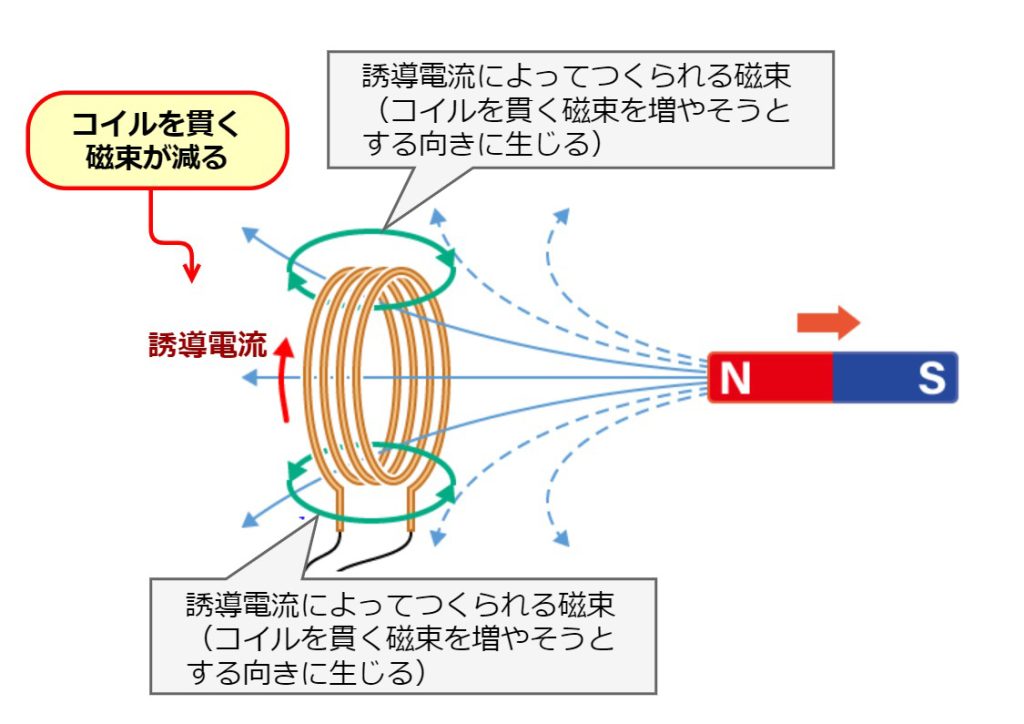
磁石をコイルから遠ざけてみます。(磁石をコイルから遠ざけると、コイルを貫く磁束が変化(減少)するので電磁誘導が起こります。)
結論として、誘導起電力によって流れる誘導電流は、コイルを貫く磁束が変化するのを妨げるような磁束を生じさせる向きに流れます。さて、電磁誘導によって発生する誘導起電力は、電磁誘導に関する次のファラデーの法則によって定義されています。
ファラデーの法則
電磁誘導によって発生する誘導起電力は、コイルを貫く磁束の単位時間あたりの変化に比例します。これを電磁誘導に関するファラデーの法則という。\(\it{N}\)回巻きのコイルを貫く磁束が時間\(Δt[s]\)の間に\(ΔΦ[Wb]\)変化したとすると、このときに発生する誘導起電力 \(e[V]\)は、次の式で表される。
\(\Large{e=-\frac{ΔΦ}{Δt}}\)
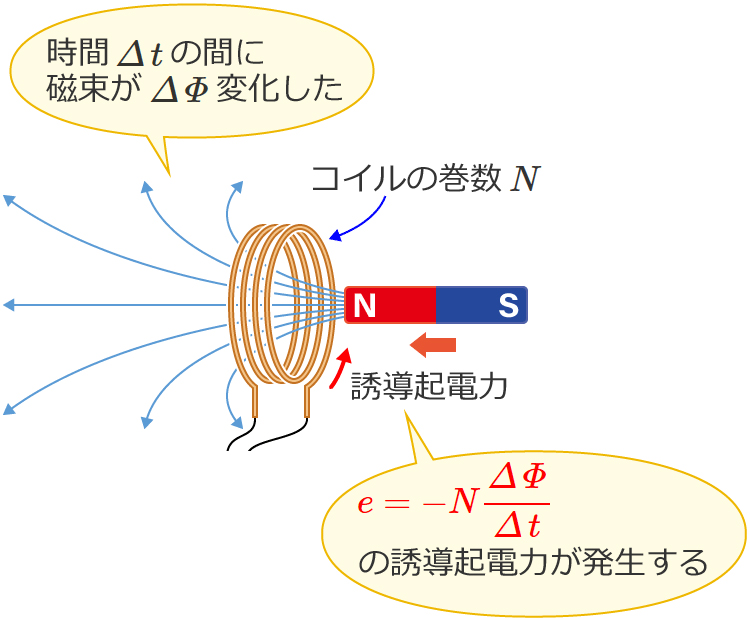
コイルの巻数と誘導起電力の大きさ
\(\Large{e=-N\frac{ΔΦ}{Δt}}\)
すなわち、電磁誘導によって発生する誘導起電力\(\it{e}\) の大きさはコイルの巻数\(\it{N}\) に比例するので、コイルの巻数 \(\it{N}\)を大きくする(巻数を多くする)と誘導起電力 \(\it{e}\)の大きさは大きくなり、コイルの巻数\(\it{N}\)を小さくする(巻数を少なくする)と誘導起電力 \(\it{e}\) の大きさは小さくなります。
コイルを貫く磁束の変化と誘導起電力の大きさ
\(\Large{e=-N\frac{ΔΦ}{Δt}}\)
すなわち、電磁誘導によって発生する誘導起電力 \(\it{e}\) の大きさはコイルを貫く磁束の変化 \(ΔΦ\) に比例するので、コイルを貫く磁束の変化 \(ΔΦ\) を大きくする(磁束の変化の差を大きくする)と誘導起電力 \(\it{e}\) の大きさは大きくなり、コイルを貫く磁束の変化 \(ΔΦ\) を小さくする(磁束の変化の差を小さくする)と誘導起電力 \(\it{e}\) の大きさは小さくなります。
また、 \(ΔΦ\)=0 のときは\(\it{e}\) =0 になるので、磁束の変化がない場合(磁束が変化しない場合)は誘導起電力は発生しません。
磁束が変化しない場合とは‥磁石とコイルを動かさないでどちらも静止させている場合
磁束が変化する間の時間と誘導起電力の大きさ
\(\Large{e=-N\frac{ΔΦ}{Δt}}\)
すなわち、電磁誘導によって発生する誘導起電力 \(\it{e}\) の大きさは磁束が変化する間の時間 \(Δt\) に反比例するので、磁束が変化する間の時間 \(Δt\) を大きくする(磁石をゆっくり動かす)と誘導起電力 \(\it{e}\) の大きさは小さくなり、磁束が変化する間の時間 \(Δt\) を小さくする(磁石を素早く動かす)と誘導起電力 \(\it{e}\) の大きさは大きくなります。
電磁誘導によって発生する誘導起電力を大きくするには。
コイルの巻数を増やす
磁力が強い磁石を使う
磁石を素早く動かす
