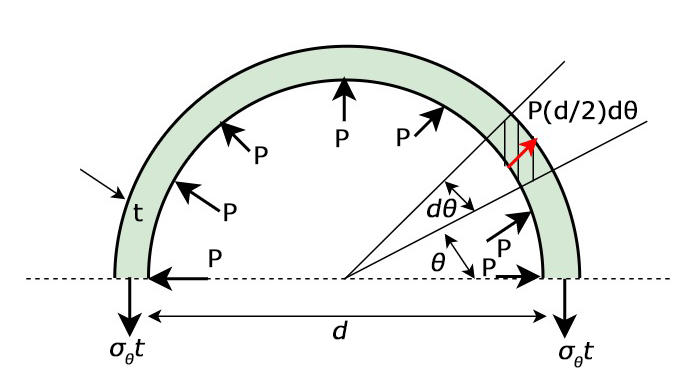
【問題】
円筒胴圧力容器とそれの鏡板に用いる板材として、円筒胴用に板厚9mm、鏡板用に板厚6mmのSM400Bがある。この板材を用いて屋外設置のR404A用高圧受液器を設計する。
ただし、R404Aの凝縮温度50℃における高圧部設計圧力は、2.21MPaとする。
(1) 設計可能な最大の円筒胴の外径\(D_{o}\)は何mmか。ただし、溶接効率は0.7とし、円筒胴外径の小数点以下は切り捨てる。
(2) (1)で求めた円筒胴に取り付ける鏡板の形状は半球形とし、この鏡板には溶接継手はないものとする。これに板厚6mmの板材を用いてもよいか。必要板厚を計算して判断せよ。ただし、円筒胴と鏡板は外径寸法を同一とする。
【解答】
(1) 設計可能な最大の円筒胴の外径\(D_{o}\)は何mmか。ただし、溶接効率は0.7とし、円筒胴外径の小数点以下は切り捨てる。
| 腐れしろ: 許容引張応力: 溶接効率: 円筒胴板厚: 設計圧力: 円筒胴内径: | 屋外設置で \(α=1㎜\) とする SM400Bなので、\(σ_{a}=100N/㎜^{2}\)とする \(η=0.7\) \(t_{a}=9㎜\) \(P=2.21MP_{a}\) \(D_{i}\) |
とすると基本式 \(P=\frac{\Large{2σ_{a}・η(t_{a}-α)}}{\Large{D_{i}+1.2(t_{a}-α)}}\)より
\(D_{i}=\frac{\Large{(2σ_{a}・η-1.2P)(t_{a}-α)}}{P}\) この式に上記数値を代入して、
\(D_{i}=\frac{\Large{(2・100・0.7-1.2・2.21)×(9-1)}}{\Large{2.21}}=497.18733\)
小数点以下切り捨てると \(D_{i}=497㎜\)
外径\(D_{o}=D_{i}+2・t_{a}=497+2・9=515㎜\)
(2) (1)で求めた円筒胴に取り付ける鏡板の形状は半球形とし、この鏡板には溶接継手はないものとする。これに板厚6mmの板材を用いてもよいか。必要板厚を計算して判断せよ。ただし、円筒胴と鏡板は外径寸法を同一とする。
| 腐れしろ: 全半球形に関する係数: 溶接効率: 鏡板板厚: 設計圧力: 鏡板半径: 許容引張応力: | 屋外設置で \(α=1㎜\) とする \(W\) \(η\) \(t_{a}\) \(P=2.21MP_{a}\) \(R\) SM400Bなので、\(σ_{a}=100N/㎜^{2}\)とする |
鏡板の最小必要板厚計算の基本式
\(t_{a}=\frac{PRW}{\Large{2・σ_{a}・η-0.2・P}} +α\)
ここで、\(W\)は全半球なので1、\(η\)は溶接継手が無いので1、円筒胴と鏡板は外径寸法を同一なので鏡板半径\(R\)は\(R=\frac{\Large{D_{o}-2・鏡板板厚}}{\Large{2}} =\frac{\Large{515-2・6}}{\Large{2}}=251.5\) この数値を代入して鏡板の最小必要板厚を計算する。
\(t_{a}=\frac{PRW}{\Large{2・σ_{a}・η-0.2・P}} +α=\frac{\Large{2.21・251.5・1}}{\Large{2・100・1-0.2・2.21}} +1=3.78523≒3.79\)
最小必要板厚は3.79㎜なので板厚6ミリの板材は使える。
次のテキストも参考にしました