【問題】
下記仕様の鋼板がある。この鋼板を用いて、屋外に設置して凝縮温度 55℃ で運転される R 404A 用高圧受液器を設計したい。この高圧受液器について、次の(1)から(3)の問に答えよ。
ただし、R 404A 冷凍装置の凝縮温度 55℃ における高圧部設計圧力は 2.48 MPa を使用するものとする。
| 鋼板の仕様; 使用鋼板 円筒胴に使用する鋼板の厚さ 鏡板に使用する鋼板の厚さ | SM400B \(t_{a1}=8 ㎜\) \(t_{a2}=8 ㎜\) |
(1) 設計可能な最大の円筒胴の外径 Do は何 mm か。
ただし、溶接継手の効率は 0.70 とし、円筒胴の外径を整数値で求めよ。
(2) (1)で求めた円筒胴に取り付ける鏡板の形状を半球形とし、この鏡板には溶接継手はないものとする。これに板厚 8 mm の鋼板を使用できる理由を、必要板厚を計算して説明せよ。
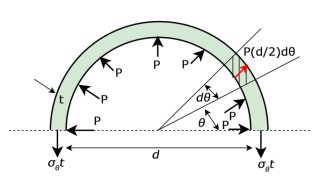
(3) この高圧受液器に使用する板厚 8 mm の半球形鏡板の内面に設計圧力 2.48 MPa が作用した場合、半球面の接線方向に誘起される引張応力 \(σ_{t}(\small{N/mm^{2}})\)を求めよ(小数点以下第1位までとする)。
【解答】
(1) 設計可能な最大の円筒胴の外径 \(D_{o}\) は何 mm か。
ただし、溶接継手の効率は 0.70 とし、円筒胴の外径を整数値で求めよ。
円筒胴に関する公式
円筒胴:\(t_{a1}=\large{\frac{PD_{i}}{2σ_{a}η-1.2P}}+α\)
\(t_{a}\):板必要厚さ \(D_{i}\):胴内径 \(σ_{a}\) : 接線方向引張応力 η:溶接継手効率 P:設計圧力 \(α\):腐れしろ
上記公式を変形すると
\(D_{i}=\large{\frac{(t_{a1}-α)(2σ_{a}η-1.2P)}{P}}\)
外径 \(D_{o}\)は
\(D_{o}=D_{i}+2t_{a1}\)
腐れしろ\(α\) : 屋外設置なので、\(α\) = 1
接線方向引張応力\(σ_{a}\) : SM400B鋼板なので、\(σ_{a}=100N/mm^{2}\)である
数値を代入して円筒胴の内径 \(D_{i}\)を求める
\(D_{i}=\Large{\frac{(8-1)(2*100*0.7-1.2*2.48)}{2.48}}=386.76129\)
円筒胴の内径 \(D_{i}\)は整数値で386㎜である
よって円筒胴外径 \(D_{o}\)は
\(D_{o}=D_{i}+2t_{ai}=386+2*8=402\)㎜
(2) (1)で求めた円筒胴に取り付ける鏡板の形状を半球形とし、この鏡板には溶接継手はないものとする。これに板厚 8 mm の鋼板を使用できる理由を、必要板厚を計算して説明せよ。
鏡板に関する公式
鏡板:\(t_{a}=\frac{PRW}{2σ_{a}η-0.2P}+α\)
\(t_{a}\):板必要厚さ \(σ_{a}\) : 接線方向引張応力 η:溶接継手効率 P:設計圧力 \(α\):腐れしろ
腐れしろ\(α\) : 屋外設置なので、\(α\) = 1
接線方向引張応力\(σ_{a}\) : SM400B鋼板なので、\(σ_{a}=100N/mm^{2}\)である
鏡板半径\(R\)は上記で求めた\(D_{i}\)の1/2で 193㎜
数値を代入して鏡板の必要板厚は
\(t_{a}=\large{\frac{PRW}{2σ_{a}η-0.2P}+α}=\large{\frac{2.48*193*1}{2*100*1-0.2*2.48}+1}=3.45406\)
よって数値を切り上げて4㎜となり8㎜の鋼板は使用可能である
(3) この高圧受液器に使用する板厚 8 mm の半球形鏡板の内面に設計圧力 2.48 MPa が作用した場合、半球面の接線方向に誘起される引張応力 \(σ_{t}(\small{N/mm^{2}})\)を求めよ(小数点以下第1位までとする)。
鏡板に関する公式
鏡板接線方向引張応力 :\(σ_{t}=\large{\frac{PRW}{2t_{a2}}}\)
\(t_{a2}\):鏡板厚さ
\(σ_{t}\) : 接線方向引張応力
P:設計圧力 R : 半径
数値を代入する
\(σ_{t}=\large{\frac{PRW}{2t_{a2}}}=\large{\frac{2.48*193*1}{2*8}}=29.915\)
よって引張応力 \(σ_{t}\)は \(29.9\small{N/mm^{2}}\)