【問題】
R22コンパウンド圧縮機を用いた二段圧縮一段膨張冷凍装置を、下記の冷凍サイクルの条件で運転する。
ただし、圧縮機の機械的摩擦損失仕事は熱として冷媒に加わるものとする。また、配管での熱の出入りはないものとする。
| 【冷凍サイクルの運転条件】 | |
| 冷凍能力 | \(Φ_{o}\)=60kW |
| 低段側圧縮機吸込み蒸気の比エンタルピー | \(h_{1}\)=397 kJ/㎏ |
| 低段側圧縮機吸込み蒸気の比体積 | \(v_{1}\)=0.22 m3/㎏ |
| 理論断熱圧縮後の低段側圧縮機吐出しガスの比エンタルピー | \(h_{2}\)=439 kJ/㎏ |
| 高段側圧縮機吸込み蒸気の比エンタルピー | \(h_{3}\)=414 kJ/㎏ |
| 高段側圧縮機吸込み蒸気の比体積 | \(v_{3}\)=0.05 m3/㎏ |
| 理論断熱圧縮後の高段側圧縮機吐出しガスの比エンタルピー | \(h_{4}\)=439 kJ/㎏ |
| 中間冷却器用膨張弁直前の液の比エンタルピー | \(h_{5}\)=246 kJ/㎏ |
| 【圧縮機の効率】 | |
| 低段側と高段側の気筒数比 | a=3 |
| 体積効率(低段側、高段側とも) | \(η_{v}\)=075 |
| 断熱効率(低段側、高段側とも) | \(η_{c}\)=0.70 |
| 機械効率(低段側、高段側とも) | \(η_{m}\)=0.90 |
1.低段側冷媒循環量\(q_{mro}\)(kg/sec)と高段側冷媒循環量\(q_{mrk}\)(kg/sec)との比\(q_{mro}/q_{mrk}\)は ?
2.蒸発器入口の冷媒の比エンタルピー\(h_{8}\)(kJ/kg) は?
3.コンパウンド圧縮機の実際の駆動軸動力\(P\)(kW) は?
【解答】
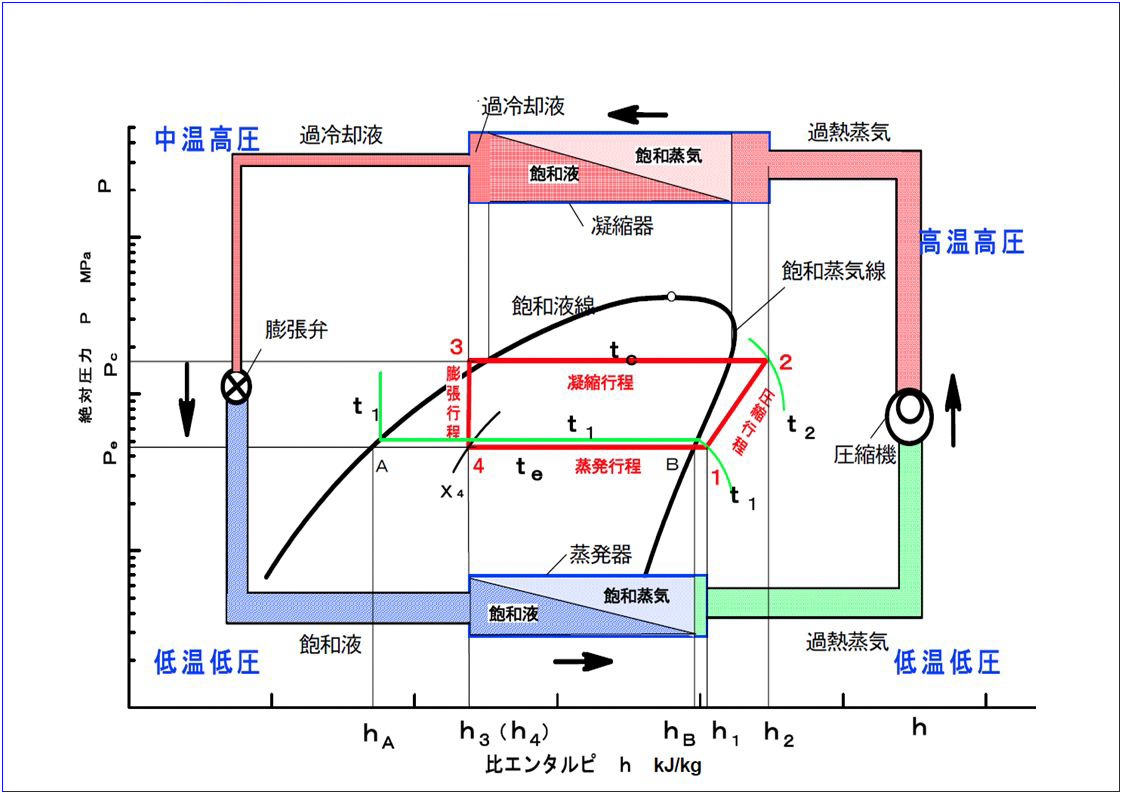
いつものように、p-h線図と冷媒の流れ概略図は次のようになる
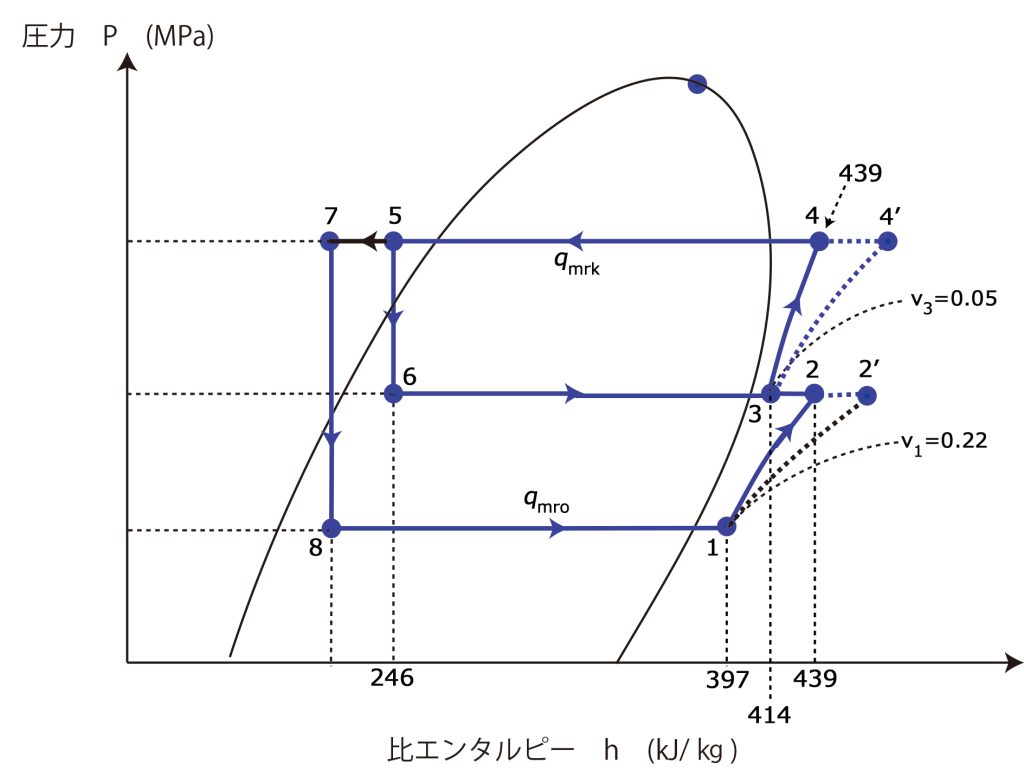
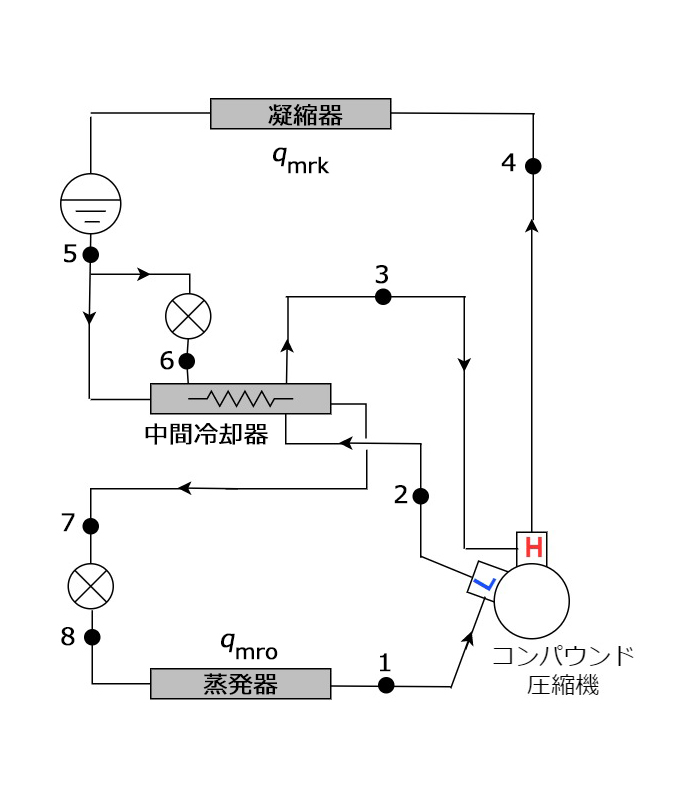
1.低段側冷媒循環量\(q_{mro}\)(kg/sec)と高段側冷媒循環量\(q_{mrk}\)(kg/sec)との比\(q_{mro}/q_{mrk}\)は ?
一般的にピストン押しのけ量(\(V\))、冷媒循環量(\(q\))、体積効率( \(η_{v}\))、比体積(\(v\))の関係式は
\(V×η_{v}=q×v\) だから
$$V_{L}=\frac{q_{mro}×v_{1}}{η_{v}} V_{H}=\frac{q_{mrk}×v_{3}}{η_{v}} $$
さて、気筒数比(a)は3なので
$$3=\frac{V_{L}}{V_{H}}=\frac{\frac{q_{mro}×v_{1}}{η_{v}} }{\frac{q_{mrk}×v_{3}}{η_{v}} }=\frac{q_{mro}×v_{1} }{q_{mrk}×v_{3}}$$
変形すると\(q_{mro}/q_{mrk}\)は
$$3×\frac{v_{3}}{v_{1}}=3×\frac{0.05}{0.22}=0.6818≒0.682$$
2.蒸発器入口の冷媒の比エンタルピー\(h_{8}\)(kJ/kg) は?
中間冷却器の熱収支を見ると
$$q_{mrk}・h_{5}+q_{mro}・\color{red}{h’}_{\color{red}{2}}=q_{mrk}・h_{3}+q_{mro}・h_{7}$$
ここで、\(\color{red}{h’_{2}}\)を使用していることに注意する。変形すると
$$q_{mro}(\color{red}{h’}_{\color{red}{2}}-h_{7})=q_{mrk}(h_{3}-h_{5})$$
さらに次のように変形する(値は前問の解答から0.682である)
$$\frac{q_{mro}}{q_{mrk}}=0.682=\frac{h_{3}-h_{5}}{h’_{2}-h_{7}} A式$$
さて、\(h_{7}\)と\(h_{8}\)は同じだから\(\color{red}{h’_{2}}\)を求めれば\(h_{8}\)が求められる
\(\color{red}{h’_{2}}\)は次の式から求められる
$$h’_{2}=h_{1}+\frac{h_{2}-h_{1}}{η_{c}・η_{m}}=397+\frac{439-397}{0.7・0.9}=463.6666≒463.7$$
上のA式に代入して\(h_{7}\)は217.3 (kJ/kg)
この問題の解説は次の「上級冷凍受験テキスト」を参考にしました
3.コンパウンド圧縮機の実際の駆動軸動力\(P\)(kW) は?
\(P=P_{L}+P_{H}\)(低段側動力と高段側動力の合計)
\(P_{L}\)と\(P_{H}\)は次の通り
$$P_{L}=\frac{q_{mro}(h_{2}-h_{1})}{η_{c}・η_{m}} P_{H}=\frac{q_{mrk}(h_{4}-h_{3})}{η_{c}・η_{m}} \color{red}{B式}$$
$$Φ_{o}=q_{mro}(h_{1}-h_{8}) q_{mro}=\frac{Φ_{o}}{h_{1}-h_{8}}=\frac{60}{397-217.3}≒0.3339$$
$$\frac{q_{mro}}{q_{mrk}}=0.6818 q_{mrk}=\frac{q_{mro}}{0.6818}≒0.4897$$
上のB式に数値を代入すると
$$P_{L}=22.26 P_{H}=19.43253968$$
$$P=P_{L}+P_{H}=41.6925368≒41.7 (kW)$$
お疲れ様でした
何はともあれ、やはり中間冷却器の熱収支が大事です