問題 1
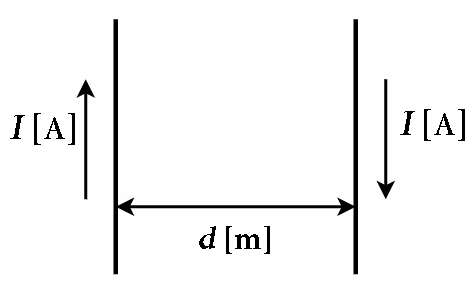
図のように、2本の長い電線が、電線間の距離 \(d\)[ m ]で平行に置かれている。両電線に直流電流 \(I\)[ A ]が互いに逆方向に流れている場合、これらの電線間に働く電磁力は。
1 .\(\Large{\frac{I} {d}}\) に比例する吸引力
2 .\(\Large{\frac{I}{d^{2}}}\) に比例する反発力
3 .\(\Large{\frac{I^{2}}{d}}\) に比例する反発力
4 .\(\Large{\frac{I^{3}}{d^{2}}}\) に比例する吸引力
解答
2本の電線に流れる電流の向きが反対の時、磁束は、電線間は密になり、外側は疎になります。このことによって、互いに反発しあう電磁力F[N](斥力)が発生します。斥力の求め方は下記の通り。
\(F=\Large{\frac{μI^{2}}{2πd}}\) [N/m]
・[N/m]:電線1mに働く力
・\(μ\):透磁率(磁束の通しやすさを表す定数)
・\(π\):定数
よって、これらの電線間に働く電磁力は、 \(\frac{I^{2}}{d}\) に比例する反発力となります。
問題 2
図の直流回路において、抵抗3Ωに流れる電流 \(I_{3}\)の値[ A ]はいくらか。
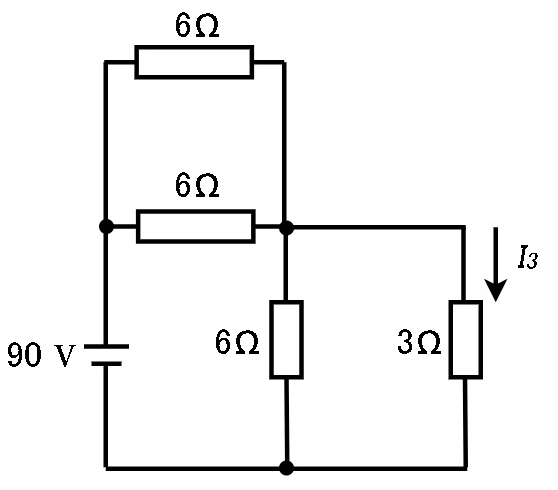
解答
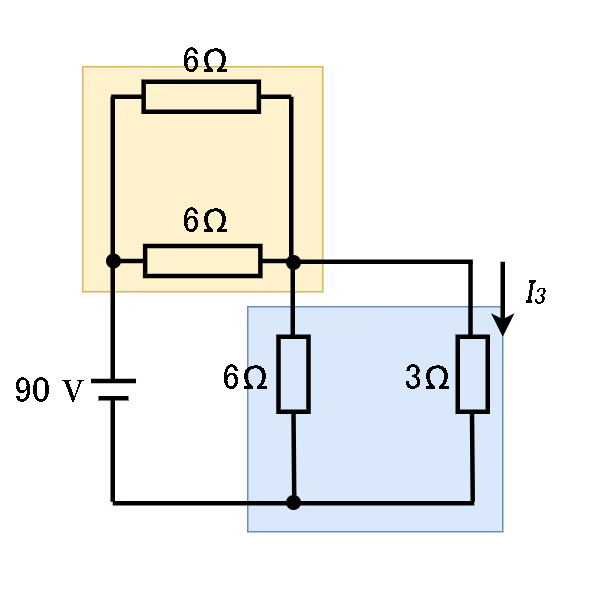
1.まず回路全体の電流の大きさを求めます。
1-1 上図のオレンジ2つの並列抵抗( 6Ω、6Ωの部分)の合成抵抗\(R_{1}\)は
\(\frac{1}{R_{1}}=\frac{1}{6}+\frac{1}{6}=\frac{1}{3}\)
\(R_{1}=3\)
1-2 上図の水色の2つの並列抵抗(6Ω、3Ωの部分)の合成抵抗\(R_{2}\)は
\(\frac{1}{R_{2}}=\frac{1}{6}+\frac{1}{3}=\frac{1}{2}\)
\(R_{2}=2\)
1-3. 回路全体の合成抵抗は、
3(Ω)+2(Ω)=5(Ω)
2.全体を流れる電流はオームの法則から
90(V)/5(Ω)=18(A)
3.\(I_{3}\)は、2抵抗の分流の比の計算。
\(I_{3}=18×\frac{6}{(3+6)}=12(A)\)
問題 3
図のような交流回路において、電源が電圧 100 V、周波数が 50 Hzのとき、誘導性リアクタンス XL=0.6 Ω、容量性リアクタンス XC=12 Ωである。この回路の電源を電圧 100 V、周波数 60 Hzに変更した場合、回路のインピーダンス[ Ω ]の値は。
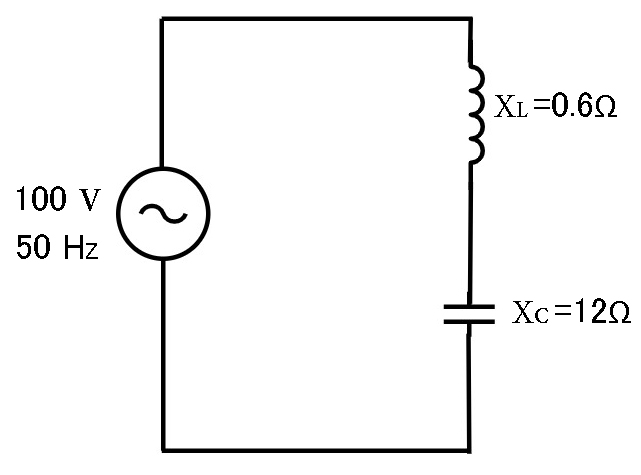
解答
●リアクタンスのおさらい
リアクタンスには、誘導性リアクタンスと容量性リアクタンスがあって、コイルのリアクタンスは誘導性リアクタンス、コンデンサのリアクタンスは容量性リアクタンスになります
1.コイルのリアクタンス(誘導性リアクタンス)
\(X_{L}\) : コイルのリアクタンス Ω
\(f\) : 電源の周波数 HZ
\(L\) : コイルのインダクタンス H(ヘンリー)
とすると
\(X_{L}=2πfL\) となり周波数に比例する
インダクタンスは周波数で変わらない、リアクタンスは周波数で変わる
コイルのインダクタンス Lの値は、コイルの固有の値(コイルごとに決まる値)なので、電源の周波数 f が変わったとしても、インダクタンス L の値は変わりません。
しかし、リアクタンス \(X_{L}\) は、\(X_{L}=2πfL\) なので、電源の周波数 f によりその大きさが変わります。
2.コンデンサのリアクタンス(容量性リアクタンス)
\(X_{C}\) : コンデンサのリアクタンス Ω
\(f\) : 電源の周波数 HZ
\(C\) : コンデンサの静電容量 F(ファラド)
とすると
\(X_{C}=\frac{1}{2πfC}\) となり、周波数に反比例する。
さて、問題は周波数 を50 Hzから60 Hzに変更した場合の回路全体のインピーダンス[ Ω ]を求めるので
誘導性リアクタンス:60/50倍
容量性リアクタンス:50/60倍 になるから、それぞれ求めると
誘導性リアクタンスは \(0.6×\frac{60}{50}=0.72\)
容量性リアクタンスは \(12×\frac{50}{60}=10\)
さて、最後に誘導性リアクタンスと容量性リアクタンスはそれぞれ打ち消し合うので、その差が回路全体のインピーダンスになる。
答え 9.28 [ Ω ]
問題 4
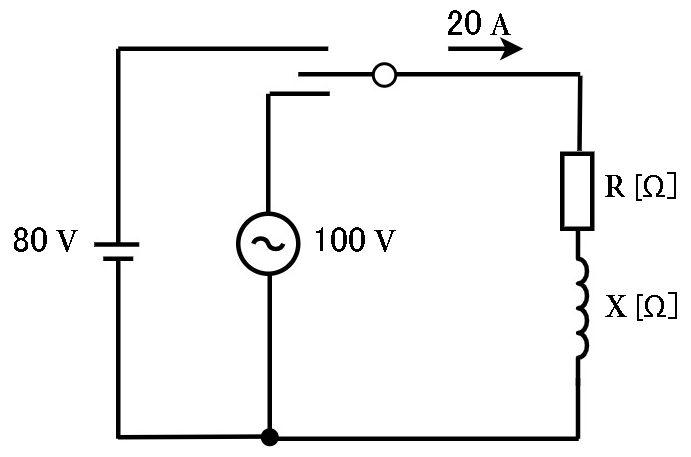
図のような回路において、直流電圧 \(80 V\)を加えたとき、\(20 A\)の電流が流れた。次に正弦波交流電圧 \(100 V\)を加えても、\(20 A\)の電流が流れた。リアクタンス\( X[ Ω ]\)の値は。
解答
1.抵抗Rを求める
直流電圧\(80V\)の時に\(20A\)の電流が流れている。
また、直流の時は、リアクタンス\(X=0 Ω\)
オームの法則から \(R=\frac{80}{20}=4 Ω\)
2.交流電圧\(100V\)に切り替え。その時\(20A\)流れている。
回路全体のインピーダンス\(Z=\frac{100}{20}=5(Ω)\)
X,Z,Rの関係式は、次の通り
\(Z=\sqrt{R^{2}+X^{2}}\)
よって
\(X=\sqrt{Z^{2}-R^{2}}=\sqrt{5^{2}-4^{2}}=3(Ω)\)





