問題 5
図のような三相交流回路において、電源電圧は \(200 V\)、抵抗は\(8Ω\)、リアクタンスは\(6Ω\)である。この回路に関して誤っているものは。
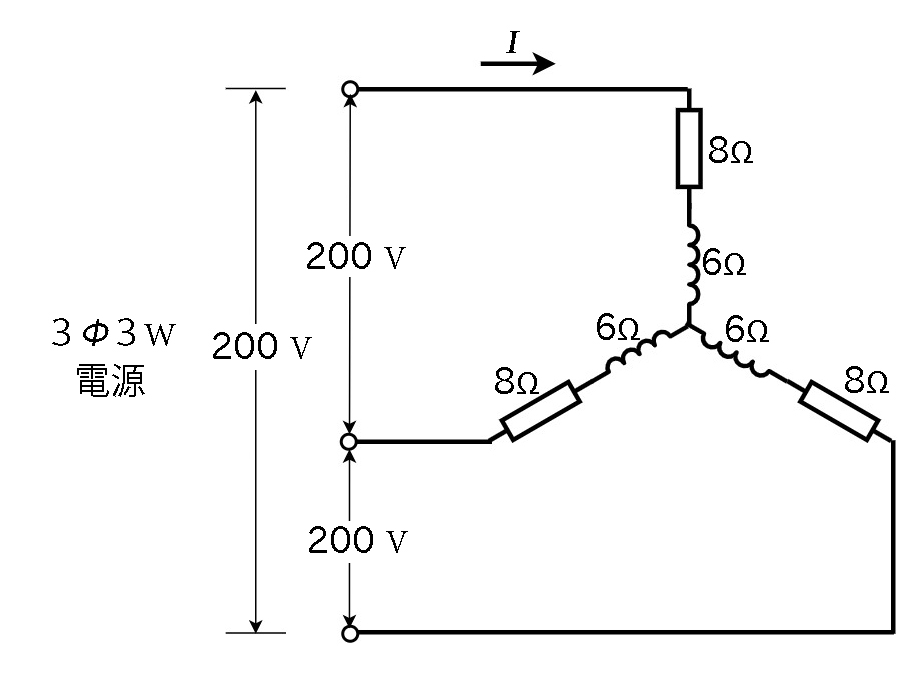
a) 1相当たりのインピーダンスは、\(10 Ω\)である。
b) 線電流\(I\) は、\(10 A\)である。
c) 回路の消費電力は、3200 Wである。
d) 回路の無効電力は、2400 varである。
解答
a)1相当たりのインピーダンス\(Z\)
\(Z=\sqrt{R^{2}+x^{2}}=\sqrt{8^{2}+6^{2}}=10\)
b)線電流\(I\)
相電圧\(V_{P}\)は \(V_{P}=\frac{200}{\sqrt{3}}\)
線電流\(I\)は \(I=\frac{V_{P}}{Z}=\frac{\frac{200}{\sqrt{3}}}{10}=\frac{20}{\sqrt{3}}≒11.55\)
c)回路の消費電力\(P\)
\(P=3×I^{2}×R=3×\frac{20^{2}}{\sqrt{3}^{2}}×8=3200\)
d) 回路の無効電力\(Q\)
Z,R,Xの関係は、X:R:Z=6:8:10=3:4:5
皮相電力を\(S\)とすると、Q 、P、 Sの関係式も同様になる
すなわち、
Q:P:S=3:4:5
以上から Qは2400 var
問題 6
図のように、単相2線式配電線路で、抵抗負荷 A(負荷電流 20 A )と抵抗負荷 B(負荷電流 10 A )に電気を供給している。電源電圧が 210 Vであるとき、負荷 Bの両端の電圧 VB と、この配電線路の全電力損失 PL の組合せとして、正しいものは。
ただし、1線当たりの電線の抵抗値は、図に示すようにそれぞれ 0.1 Ωとし、線路リアクタンスは無視する。
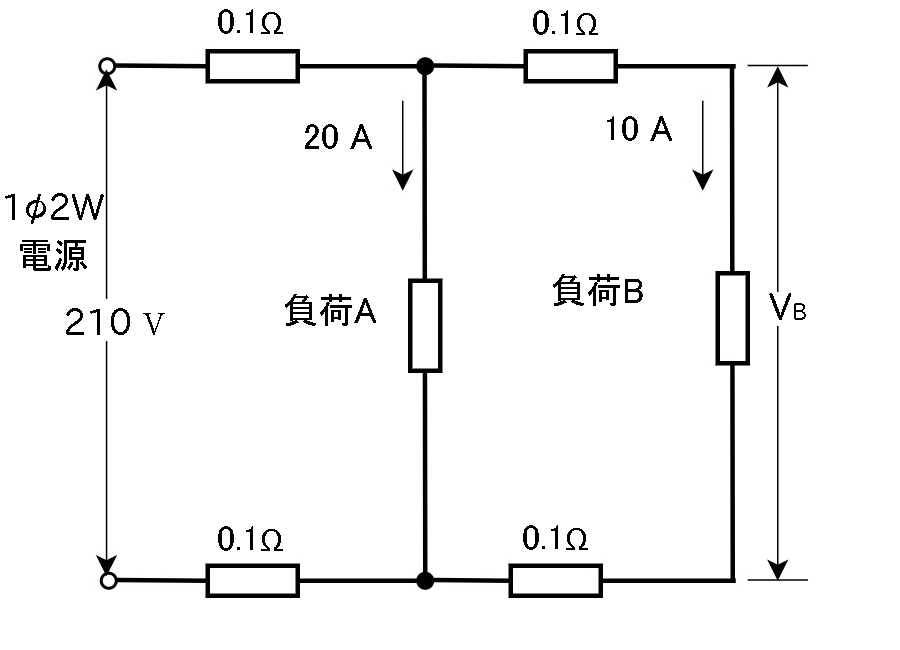
1.VB = 202 V PL = 100 W
2.VB = 202 V PL = 200 W
3.VB = 206 V PL = 100 W
4.VB = 206 V PL = 200 W
解答
a)両端の電圧\(V_{B}\)
・左上の抵抗で:\(30A×0.1Ω=3V\) 電圧降下
・右上の抵抗で:\(10A×0.1Ω=1V\) 電圧降下
・1線分で、\(3+1=4(V)\) なので、2線分として\(2×4(V)=8(V)\) の電圧降下
よって、\(V_{B}=210-8=202(V)\)
b)全電力損失\(P_{L}\)
電力 \(P=I^{2}×R\)
・左上の抵抗で:\(30^{2}×0.1=90(W)\)
・右上の抵抗で:\(10^{2}×0.1=10(W)\)
よって、1線分で、90+10=100(W) なので、
2線分として \(P_{L}=2×100(W)=200(W)\)
問題 7
ある変圧器の負荷は、有効電力\( 90 kW\)、無効電力 \(120 kvar\)、力率は \(60%\)(遅れ)である。いまここに有効電力\(70 kW\)、力率 \(100%\)の負荷を増設した場合、この変圧器にかかる負荷の容量\([kV・A]\)は。
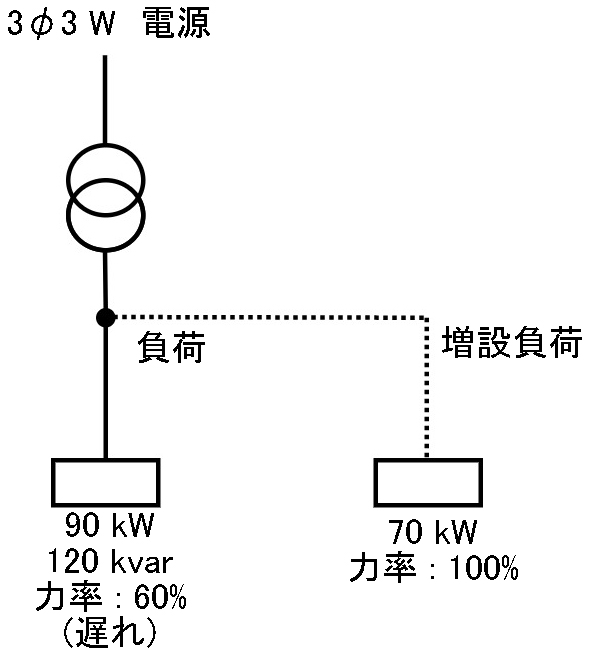
1.100
2.150
3.200
4.280
解答
負荷容量は次の式で求めることができる。
\(負荷容量=\sqrt{(有効電力)^{2}+(無効電力)^{2}}\)
問題では、有効電力\(90kW\)に、有効電力\(70kW\)を増設したので、
有効電力は\(90+70=160(kW)\)となる。
よって、\(負荷容量=\sqrt{160^2+120^{2}}=\sqrt{40000}=200(kVA)\) となる
問題 8
図のような直列リアクトルを設けた高圧進相コンデンサがある。電源電圧が\(V[ V ]\)、誘導性リアクタンスが\(9Ω\)、容量性リアクタンスが\( 150 Ω\)であるとき、この回路の無効電力(設備容量)\([var]\)を示す式は。
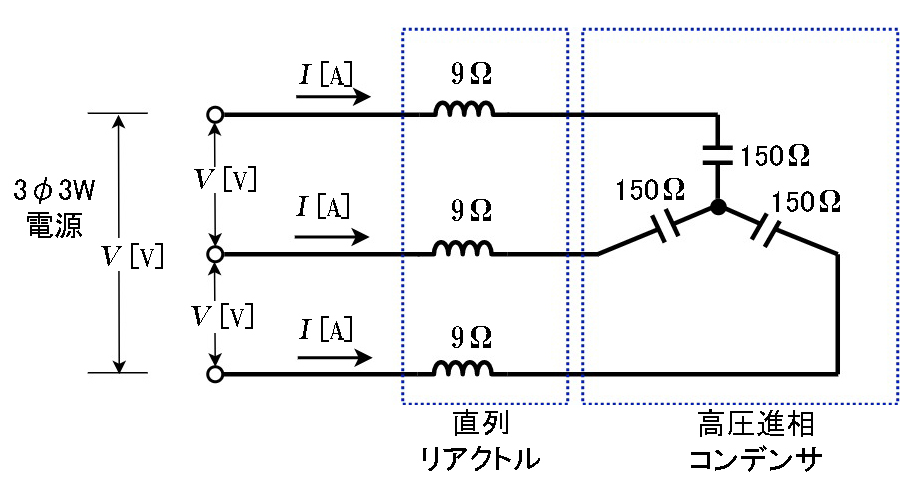
1.\(\Large{\frac{V^{2}}{159^{2}}}\)
2.\(\Large{\frac{V^{2}}{141^{2}}}\)
3.\(\Large{\frac{V^{2}}{159}}\)
4.\(\Large{\frac{V^{2}}{141}}\)
解答
a)相電圧\(V’\)
電源電圧は\(V(V)\)なので、相電圧\(V’\)は、\(V’=\frac{V}{\sqrt{3}}(V)\)
b)1相のリアクタンス\(X\)
1相のリアクタンス\(X\)は、誘導性リアクタンス\(X_{C}\)と容量性リアクタンス\(X_{L}\)が打ち消し合う、
\(X=X_{L}-X_{C}=150-9=141(Ω)\)
c)線電流\(I\)
\(I=V’×\frac{1}{X}=\frac{V}{\sqrt{3}}×\frac{1}{141}(A)\)
d)3相分の無効電力\(Q\)
\(Q=3×I^{2}×X =3×\frac{V^{2}}{\sqrt{3}^{2}}×\frac{1^{2}}{141^{2}}×141=\frac{V^{2}}{141}(var)\)





