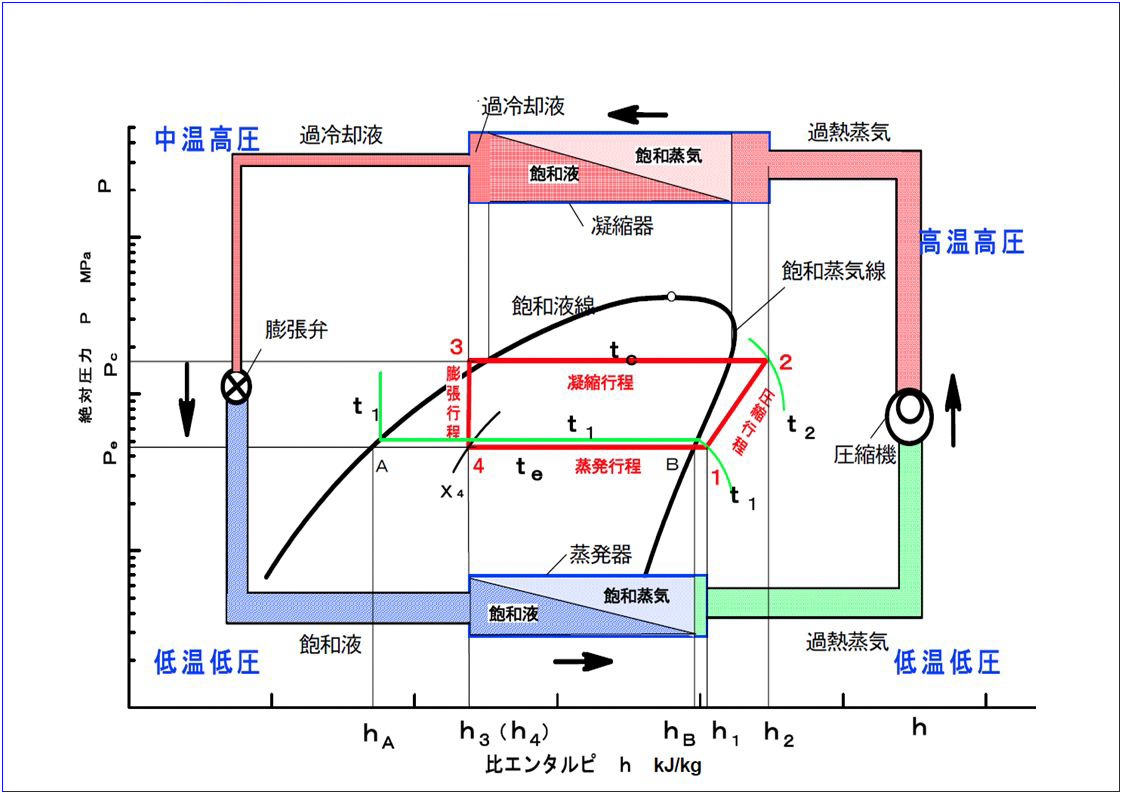
1.一般的にp-h線図は下のような線図であります。
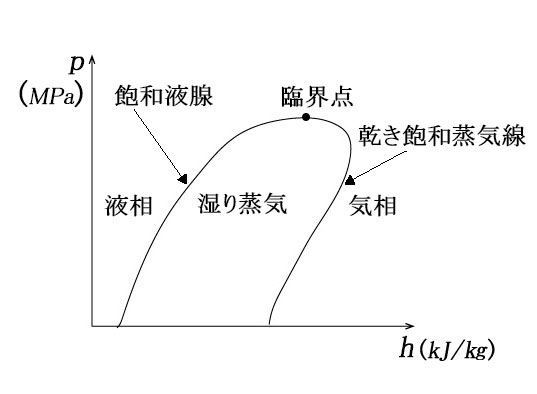
この図を説明する前に冷媒では無く1kgの水を暖める場合を考えてみると下図のような温度上昇になる。
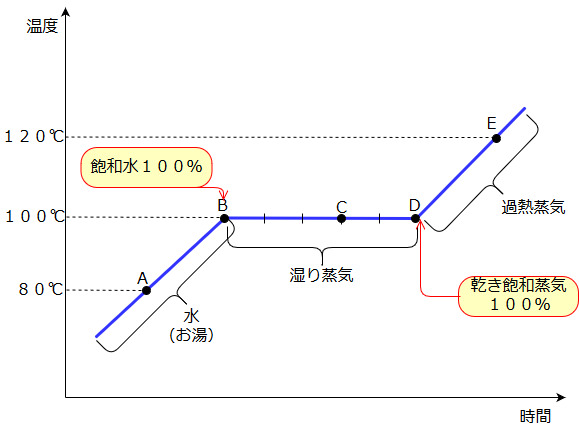
①時間とともに温度が上昇して行き、ちょうど100℃ に達したとき(点B)温度上昇が止まり、ここから水が水蒸気に変わっていく。
②沸騰している間(B~D)は熱を加えていても温度が100℃ のままで上がっていきません。このときの水や蒸気の状態を 湿り蒸気 といい、水の部分を飽和水(冷媒のときは飽和液)、蒸気の部分を乾き飽和蒸気といいます。
③そして、すべてが水蒸気になると(点D)、また温度が上昇して行きます。沸騰している間(B~D)は熱を加えていても温度が100℃ のままで上がっていきません。
この状態変化は下図のようにも表すことができます。
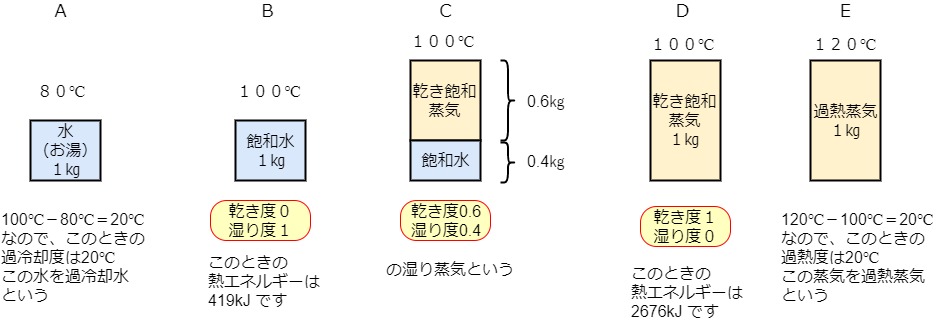
さて、これを縦軸を圧力P(単位MPa)、横軸を比エンタルピーh(単位kJ/㎏)としたp-h線図に書くと次のようになる。
※比エンタルピーとは1kgあたりのエンタルピー(熱含量とか含熱量)でこれはそのものが持っている熱エネルギーです
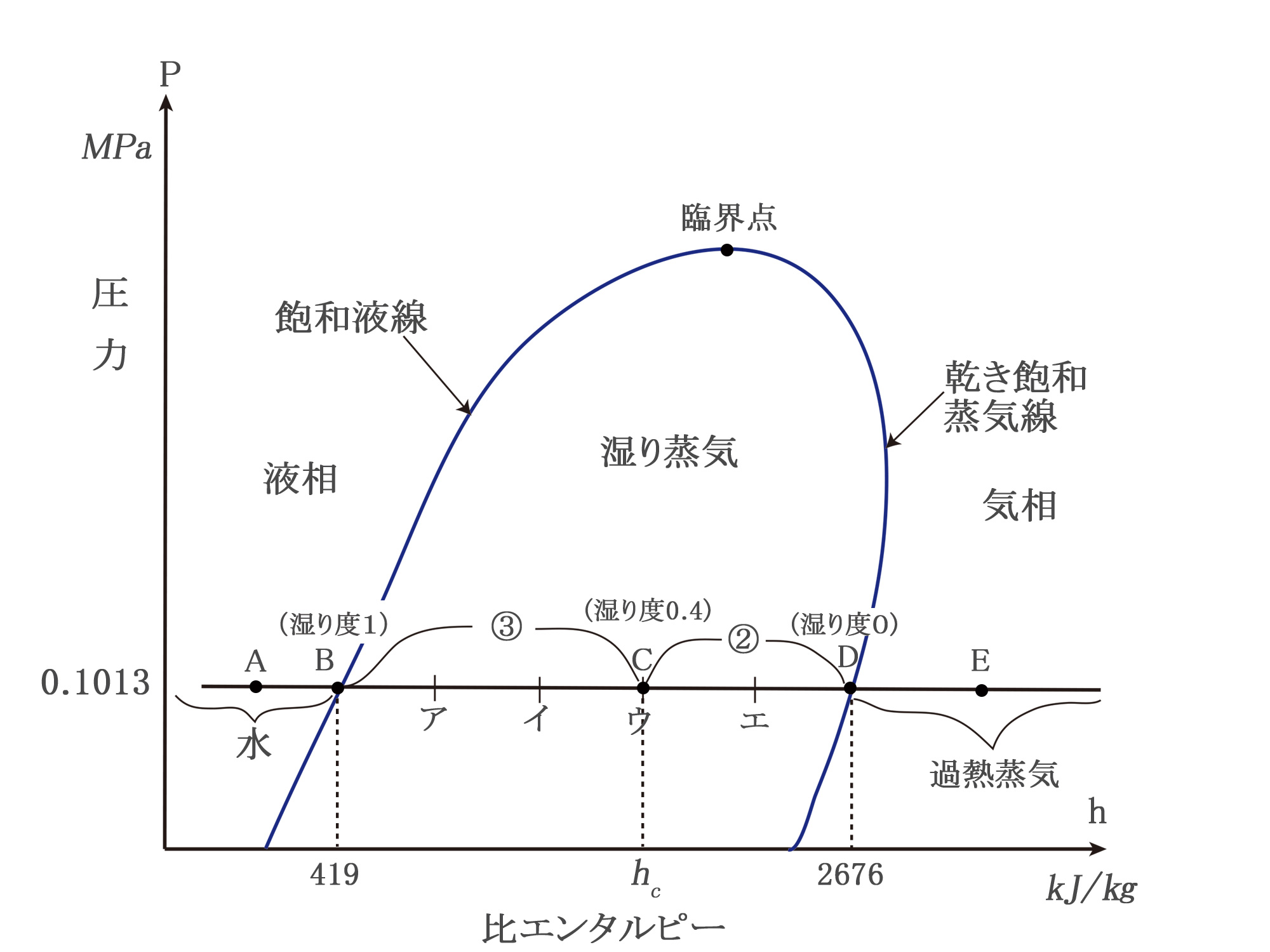
そして、点Bは湿り度1乾き度0 の飽和水、点Dは湿り度0乾き度1の乾き飽和蒸気、BD 間は湿り蒸気といい、BD 間を5等分したとき、点ア~エの湿り度と乾き度は次の表の通り。
| 湿り度 | 乾き度 | |
| ア | 0.8 | 0.2 |
| イ | 0.6 | 0.4 |
| ウ | 0.4 | 0.6 |
| エ | 0.2 | 0.8 |
以上、水の場合を考えました。次に冷凍サイクルで使用する冷媒の場合を考えてみます
2.冷凍サイクルの場合
まず冷凍サイクルとはどのような機器を使用して、どのようなサイクルになっているか?
基本的な冷凍サイクルのは次のようになります
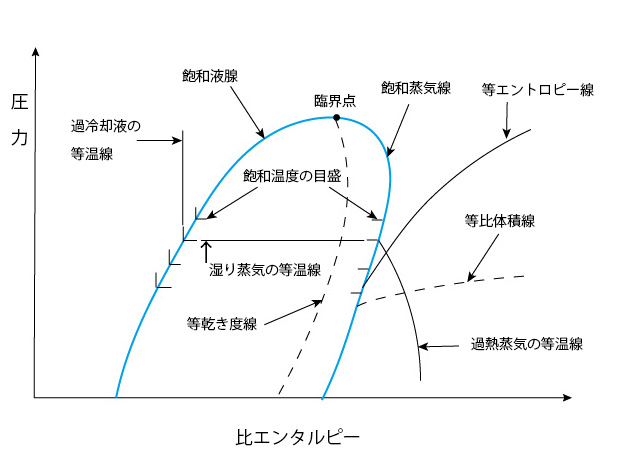
また、構成機器を含めた冷凍サイクルは次のようになります

これを、簡略化したp-h線図上に書くと次のようになります。
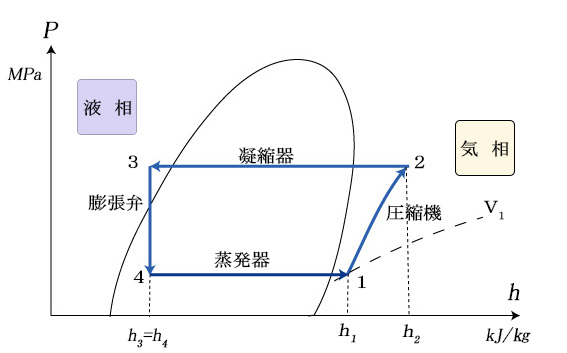
3.実際に冷凍サイクルをp-h線図上に書くことにします
冷媒はR22
| 蒸発温度 | 凝縮温度 | 膨張弁前 液温度 | 吸入ガス 温度 | 蒸発圧力 | 凝縮圧力 | 過冷却度 | 過熱度 |
| -15℃ | 30℃ | 25℃ | -10℃ | 0.296MPa abs | 1.192MPa abs | 5℃ | 5℃ |
※absはabsoluteの略で絶対真空を圧力ゼロとして絶対圧力を表す。
上の表の状態をp-h線図上に書いていきます。
3.1 凝縮器の線
飽和蒸気線、飽和液線の30℃目盛りを通る水平線①を引く(30℃の凝縮圧力1.192MPa absを通る水平線でも同じ)
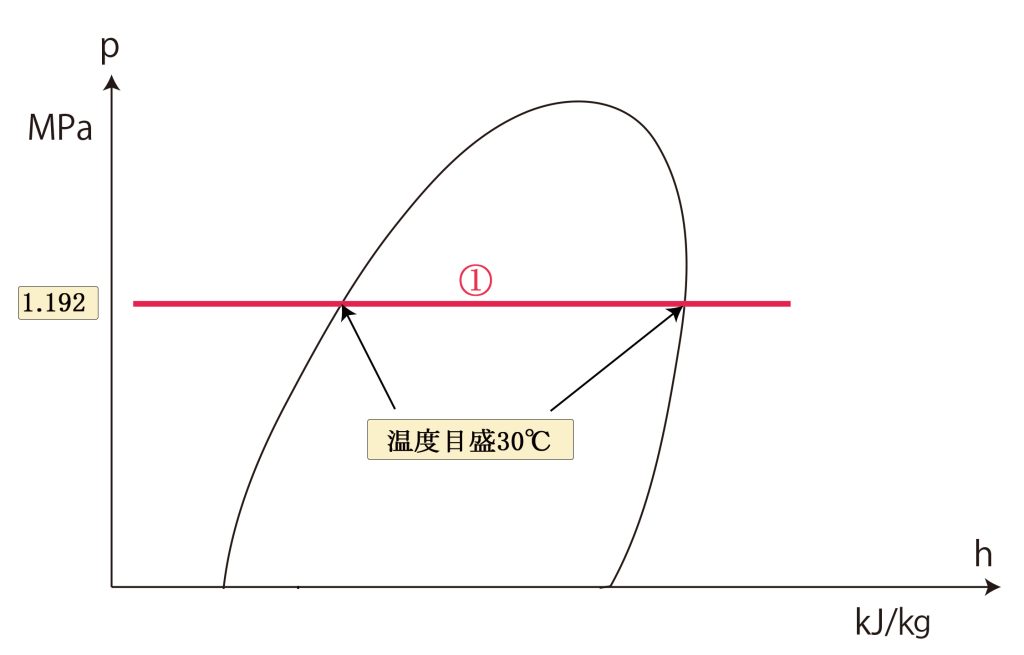
3.2 蒸発器の線
飽和蒸気線、飽和液線の-15℃目盛りを通る水平線②を引く(-15℃の蒸発圧力0.296MPa absを 通る水平線でも同じ)
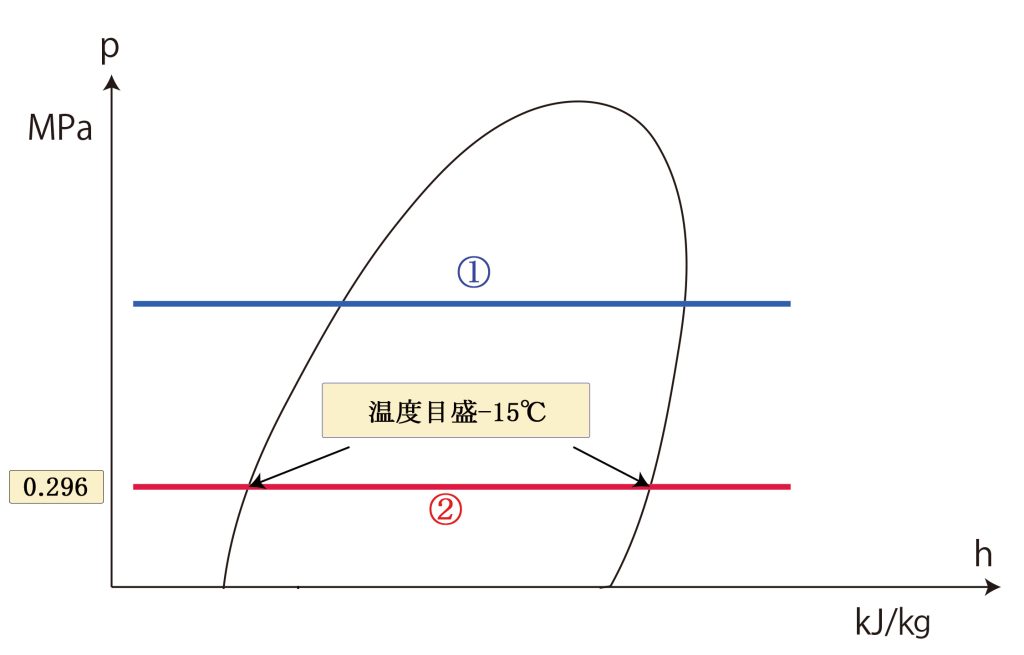
3.3 圧縮機の線
蒸発器の線②と-10℃等温線との交点(点1)は圧縮機吸込ガスの状態を示す。 点1から等エントロピー線と平行に曲線③を引く。等エントロピー線は曲線です。
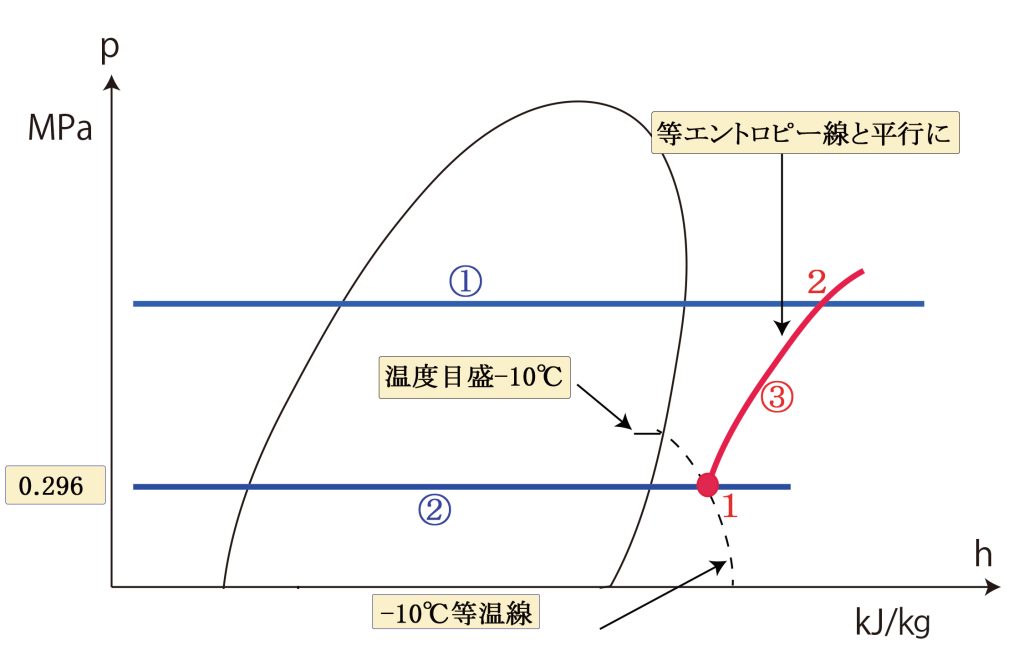
3.4 膨張弁の線
膨張弁前は25℃の過冷却液だから、飽和液線の25℃(点E)を通る垂直線④を引く。 線④と線①の交点3は膨張弁前の状態を示す(25℃の飽和圧力1.045MPa absから 点Eを求めても同じ)
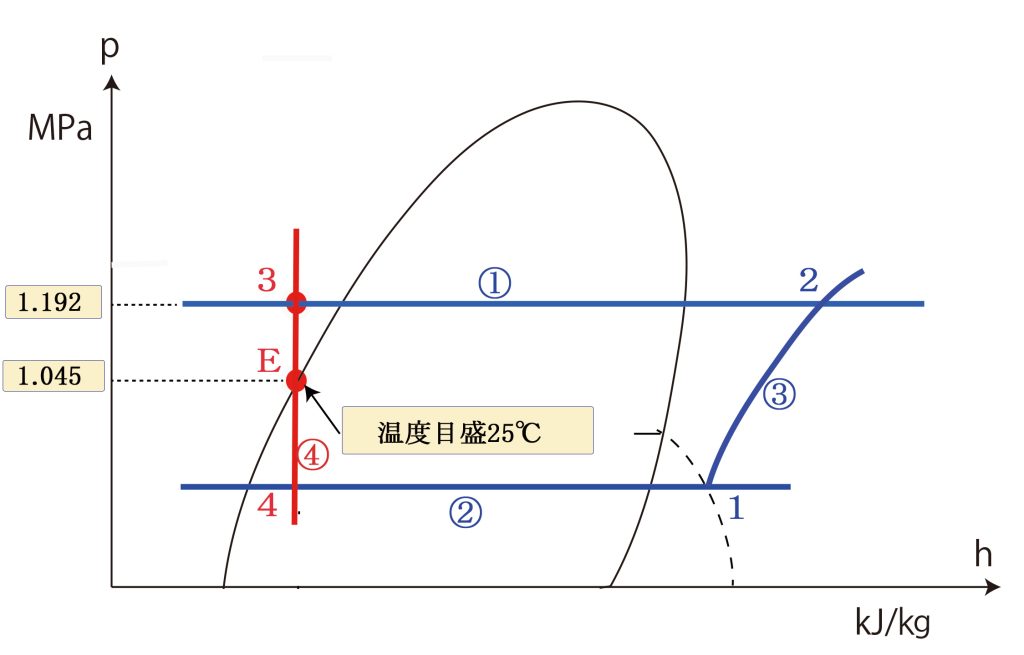
3.4 図を完成する
点1~4より外の余分な線を消して下図の様に仕上げる。
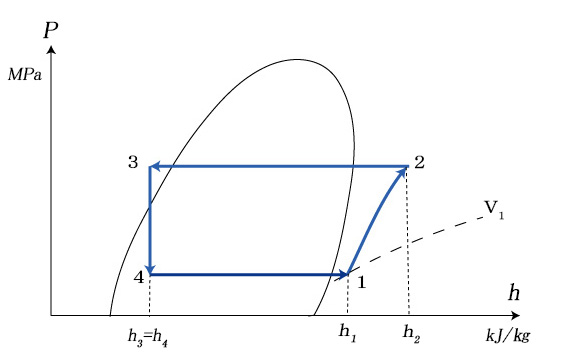
4.p-h線図上の冷凍サイクルからいろいろな状態変化を見る
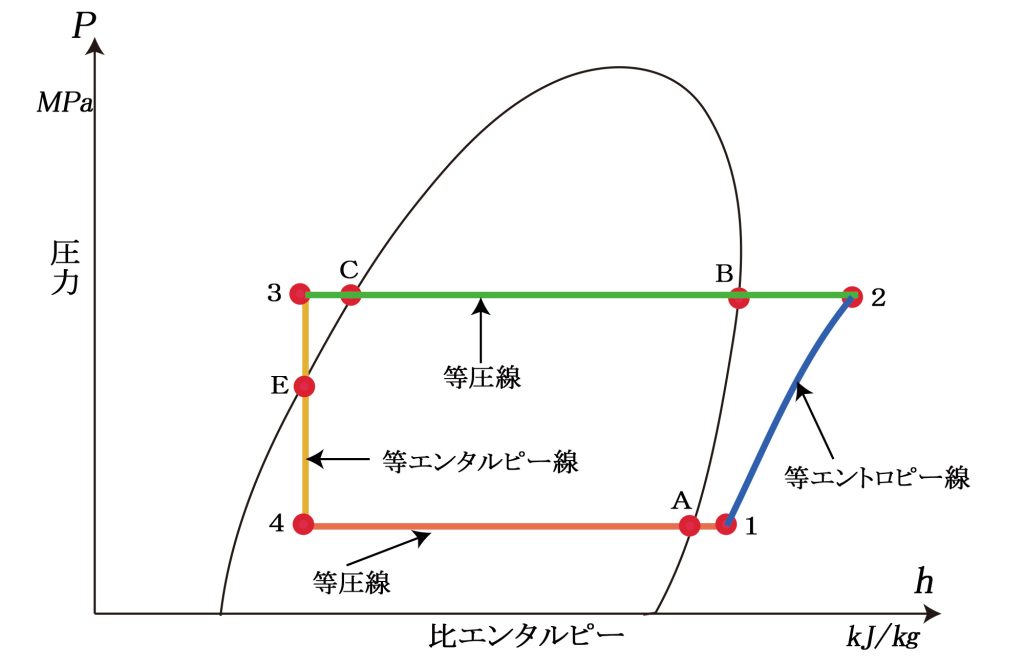
①ガスの断熱圧縮(圧縮機)
圧縮機でガスを圧縮すると「等エントロピー線」に沿って1→2へ変化する(「断熱圧縮」または「等エントロピー圧縮」と言う) 。圧縮するに従いガスの圧力と温度は上り、高温高圧の「過熱蒸気」になります。
②圧力一定の放熱(凝縮器)
2→Bは凝縮器入口近くの状態で、冷媒は「過熱蒸気」、つまり高温のガス。 B→Cで冷媒は次々に液化し「湿り蒸気」となる。液と蒸気は混在し、温度は「凝縮温度」で一定。 Cで全て液となる。C→3は「過冷却液」であり、飽和温度からの温度低下を「過冷却度」と言う。
過冷却度=凝縮温度―膨張弁前冷媒温度
③冷媒液の膨張(膨張弁)
高圧の液を急に減圧すると「等エンタルピー膨張」する。 これは膨張弁やキャピラリを流れる冷媒の変化である。 3→E(飽和液線上)間は液のままで、温度も一定。 E→4で冷媒は一部が蒸発して温度が下り、「湿り蒸気」となる。(液・ガス混在)
④圧力一定の吸熱(蒸発器)
4→Aで冷媒液は熱を吸収して次々に蒸気になる。 この間、液と蒸気は混って流れ(液・ガス混在)、温度は「蒸発温度」で一定。 Aで液は全て蒸発して飽和蒸気になる。 その蒸気は温度上昇して、蒸発器出口1では「過熱蒸気」となるのが一般的。 飽和温度からの温度上昇を「過熱度」と言う。
過熱度=圧縮機吸込ガス温度―蒸発温度
5.p-h線図例題1
下図の理論冷凍サイクルp-h線図がある。ただし、装置の冷媒循環量は540kg/hである。
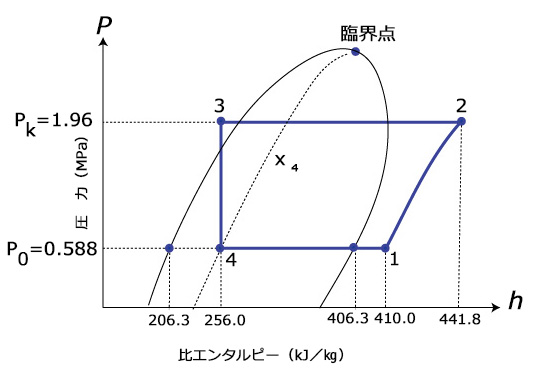
(1)冷凍能力は?(冷凍トン)
冷凍能力を計算する公式は \(Φ_{o}\)=\(q_{mr}\)(\(h_{1}\)-\(h_{4}\))
\(Φ_{o}\) : 冷凍能力(kW)
\(q_{mr}\) : 冷媒循環量(1秒間当たり)
\(h_{1}\) : 1の比エンタルピー
\(h_{4}\) : 2の比エンタルピー
これで計算すると \(Φ_{o}\)=540÷3600×(410.0-256.0)=23.1(kW)
1日本冷凍トン=3.86kWだから 23.1÷3.86≒6冷凍トン
(2)凝縮器の放熱量は?
凝縮器の放熱量\(Φ_{k}\)を計算する公式は \(Φ_{k}=Φ_{o}+p\)
一方
\(Φ_{k}=q_{mr}(h_{2}-h_{3})\)
\(p=q_{mr}(h_{2}-h_{1})\)
また\(Φ_{o}=q_{mr}(h_{1}-h_{4})\)だから \(Φ_{k}=Φ_{o}+p=q_{mr}(h_{2}-h_{4})\) \( h_{3}\)と\(h_{4}\)は同値
計算すると \(Φ_{k}\)=540÷3600×(441.8 - 256)=27.87≒27.9(kW)
(3)冷凍サイクルの成績係数は?
成績係数COPを計算する公式は COP =\(Φ_{o}/p\)
\(Φ_{o}\)は(1)より23.1kW
\(p\)=540÷3600×(441.8-410.0)=4.77kW
計算するとCOP=23.1/4.77=4.8427 ≒ 4.84
(4)蒸発器入り口の冷媒の乾き度は?
上の問題p-h線図を次のように書き直し\(h_{5}\)と\(h_{6}\)とします
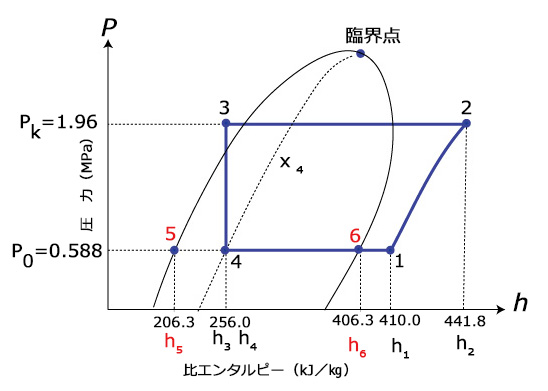
そうすると乾き度\(x_{4}\)は次の式で求められます
$$x_{4}=\frac{h_{4}-h_{5}}{h_{6}-h_{5}}$$
計算すると
$$x_{4}=\frac{256.0-206.3}{406.3-206.3}$$
乾き度は約0.25となる