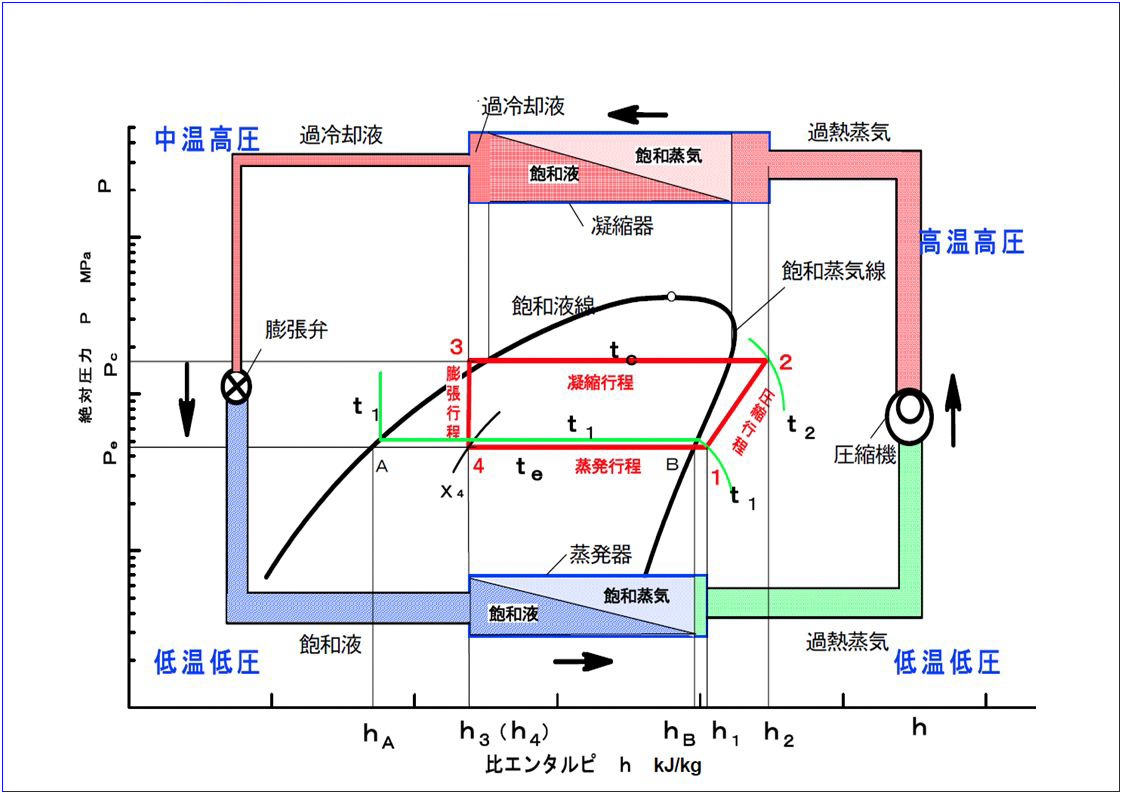
【問題】R404Aを冷媒とする二段圧縮一段膨張の冷凍装置を、下記の冷凍サイクルの運転条件で運転する。この冷凍装置の冷凍能力が150kWである。
ただし、圧縮機の損失、配管での熱の出入りおよび圧力損失はないものとする。
| 【理論冷凍サイクルの運転条件】 | |
| 低段圧縮機吸込み蒸気の比エンタルピー | \(h_{1}\)＝358 kJ/㎏ |
| 低段圧縮機の断熱圧縮後の吐出しガスの比エンタルピー | \(h_{2}\)＝378 kJ/㎏ |
| 高段圧縮機吸込み蒸気の比エンタルピー | \(h_{3}\)＝366 kJ/㎏ |
| 高段圧縮機の断熱圧縮後の吐出しガスの比エンタルピー | \(h_{4}\)＝390 kJ/㎏ |
| 中間冷却器用膨張弁直前の液の比エンタルピー | \(h_{5}\)＝240 kJ/㎏ |
| 蒸発器用膨張弁直前の液の比エンタルピー | \(h_{7}\)＝205 kJ/㎏ |
１．高段の凝縮圧力\(P_{k}\)が1.80MPa、低段の蒸発圧力\(P_{o}\)が0.20MPaであったとき、成績係数が実用上ほほ最大となり、最も適正な運転となる中間圧力\(P_{m}\)（MPa）？。ただし、圧力は絶対圧力とする。
２．中間冷却器へのバイパス冷媒循環量\(q’_{mro}\)（kg/sec）と低段側の冷媒循環量\(q_{mro}\)（kg/sec）との比 \(q’_{mro}/q_{mro}\) は。？
３．高段側の冷媒循環量\(q_{mrk}\)（kg/sec）は ？
４．成績係数(COP)\(th・R\)は ？
まず、p-h線図と機器相互の冷媒の流れ概略図を次のように書く
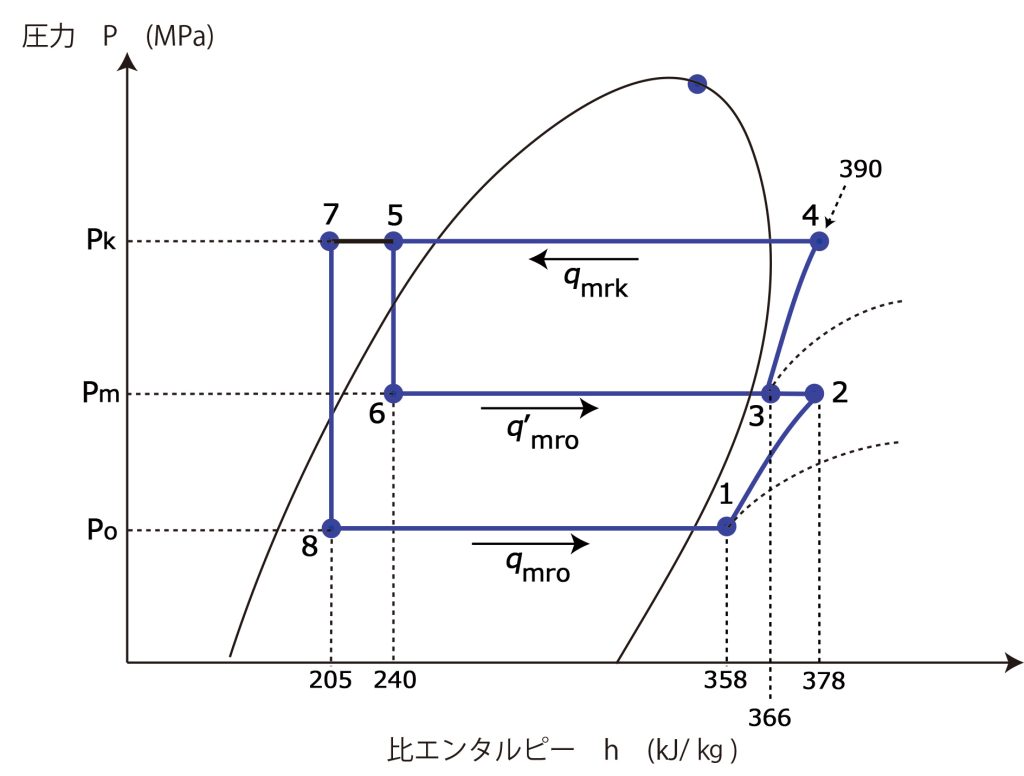
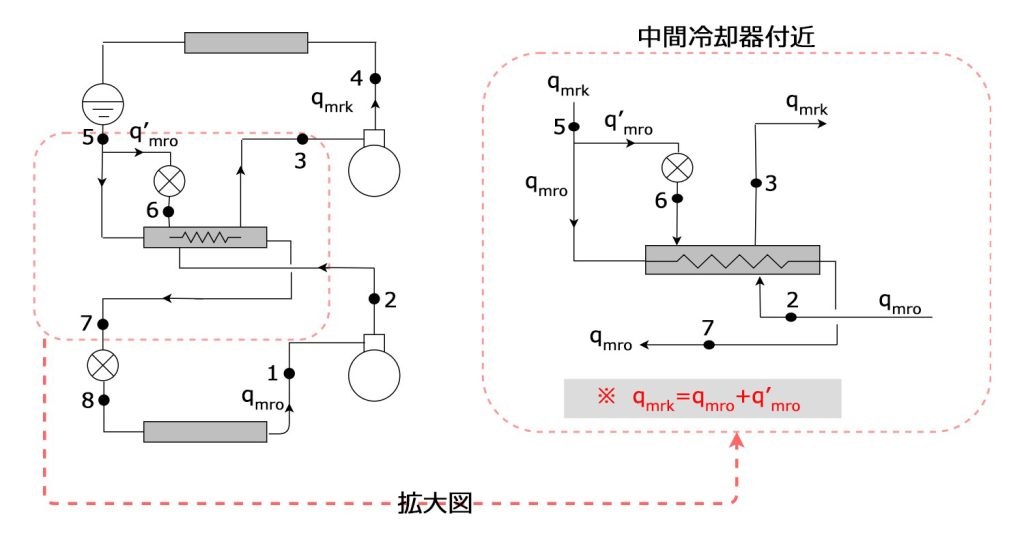
１．高段の凝縮圧力が1.80MPa、低段の蒸発圧力\(P_{o}\)が0.20MPaであったとき、成績係数が実用上ほほ最大となり、最も適正な運転となる中間圧力\(P_{m}\)（MPa）？。ただし、圧力は絶対圧力とする。
「成績係数が実用上ほほ最大となり、最も適正な運転となる中間圧力」これはいろいろなテキストに説明があると思いますが、「高段、低段の圧力比を同等にする」という説明が多いと思います。
高段、低段の圧力比とは今の場合
$$\frac{P_{k}}{P_{m}}=\frac{P_{m}}{P_{o}}$$
変形すると
数値を代入すると \(P_{m}=\sqrt{1.8・0.2}=0.6 [MPa]\)
２．中間冷却器へのバイパス冷媒循環量\(q’_{mro}\)（kg/sec）と低段側の冷媒循環量\(q_{mro}\)（kg/sec）との比 \(q’_{mro}/q_{mro}\) は。？
中間冷却器の熱収支を考えます（熱収支ですから入るもの、出るもの）
$$q_{mrk}=q_{mro}+q’_{mro} だから$$
またまた変形して {＊＊＊}×\(q’_{mro}\)={＃＃＃}×\(q_{mro}\) の形に整理すると
下のように変形して数値を代入すると
この問題の解説は次の「上級冷凍受験テキスト」を参考にしました
３．高段側の冷媒循環量\(q_{mrk}\)（kg/sec）は ？
\(q_{mrk}=q_{mro}+q’_{mro}\) だから、前問の解答から次のように変形できる
$$q_{mrk}=q_{mro}+0.373・q_{mro}$$
次に冷却能力が判っているので次の式から\(q_{mro}\)を求める
$$Φ_{o}=q_{mro}(h_{1}-h_{8})$$$$q_{mro}=\frac{Φ_{o}}{h_{1}-h_{8}}$$
４．成績係数(COP)\(th・R\)は ？
この問題は簡単ですので式だけ示しておきます。ご自身で数値を代入してください
$$(COP)th・R=\frac{Φ_{o}}{P}$$
$$ここで P=P_{L}+P_{H}$$
以上で終わり
