p-h線図例題９ 蒸発器２台

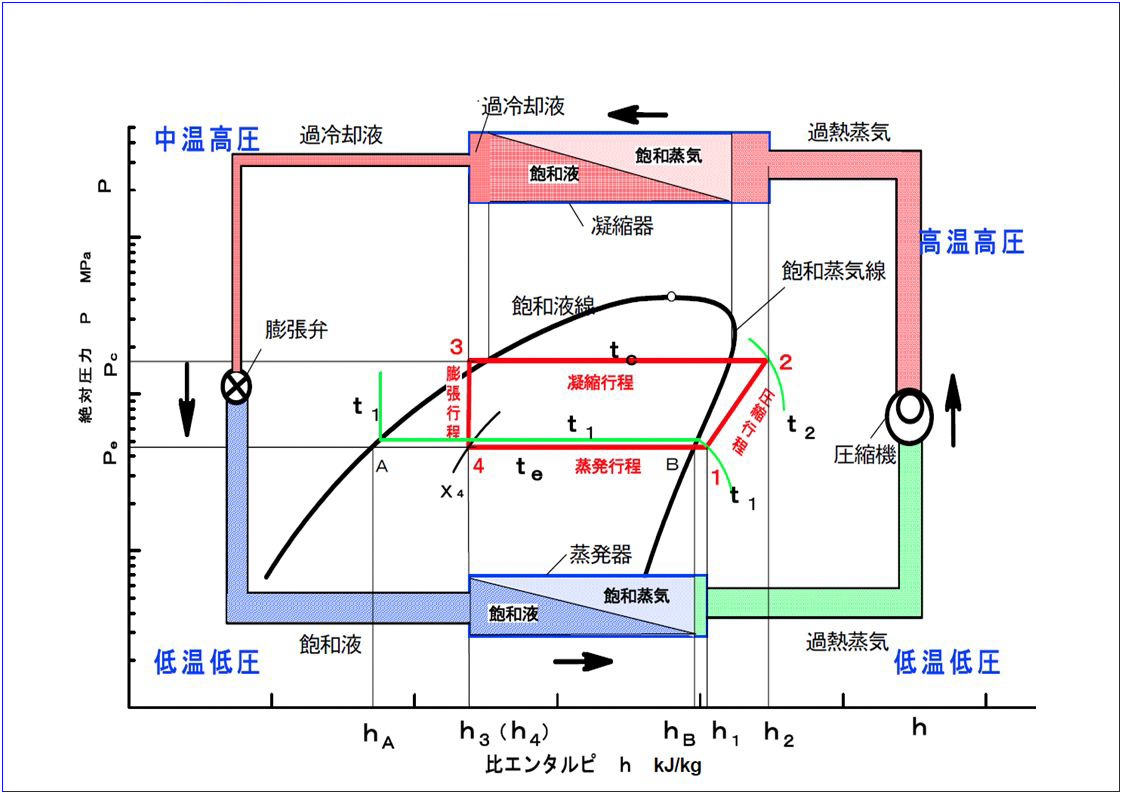
【問題】アンモニアを冷媒とする蒸発温度の異なる2台の蒸発器を1台の圧縮機で冷却する冷凍装置は、下図のとおりである。
この装置において、蒸発器Ⅰを流れる流量（kg/sec）と蒸発器Ⅱを流れる流量（kg/sec）の比は1：1である。この装置の冷凍サイクルの運転条件と圧縮機の効率は、下記のとおりである。ただし、配管での熱の出入りはないものとする。

【全負荷時の運転条件】
圧縮機断熱圧縮後の吐出しガスの比エンタルピー	$h_{2}$＝1830 kJ/㎏
膨張弁直前の比エンタルピー	$h_{3}$＝510 kJ/㎏
蒸発器Ⅰの出口冷媒の比エンタルピー	$h_{5}$＝1610 kJ/㎏
蒸発器Ⅱの出口冷媒の比エンタルピー	$h_{8}$＝1590kJ/㎏
圧縮機吸込み蒸気の比体積	_{$v_{1}$}＝0.4m³ /㎏
圧縮機の押しのけ量	$V$＝360m³ /h
【圧縮機の効率】
体積効率	$η_{v}$＝0.8
断熱効率	$η_{c}$＝0.7
機械効率	$η_{m}$＝0.9

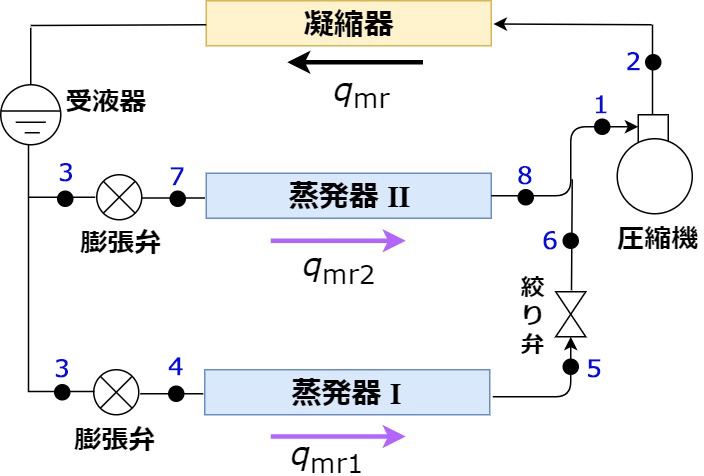
１．凝縮器を流れる実際の冷媒循環量$q_{mr}$(kg/sec)　は？

２．蒸発器Ⅰと蒸発器Ⅱの合計の実際の冷凍能力$Φ_{o}$（kW）　は？

３．圧縮機の実際の圧縮軸動力$P$（kW）は？

４．実勢の成績係数(COP)R　は？

p-h線図は次のようになる

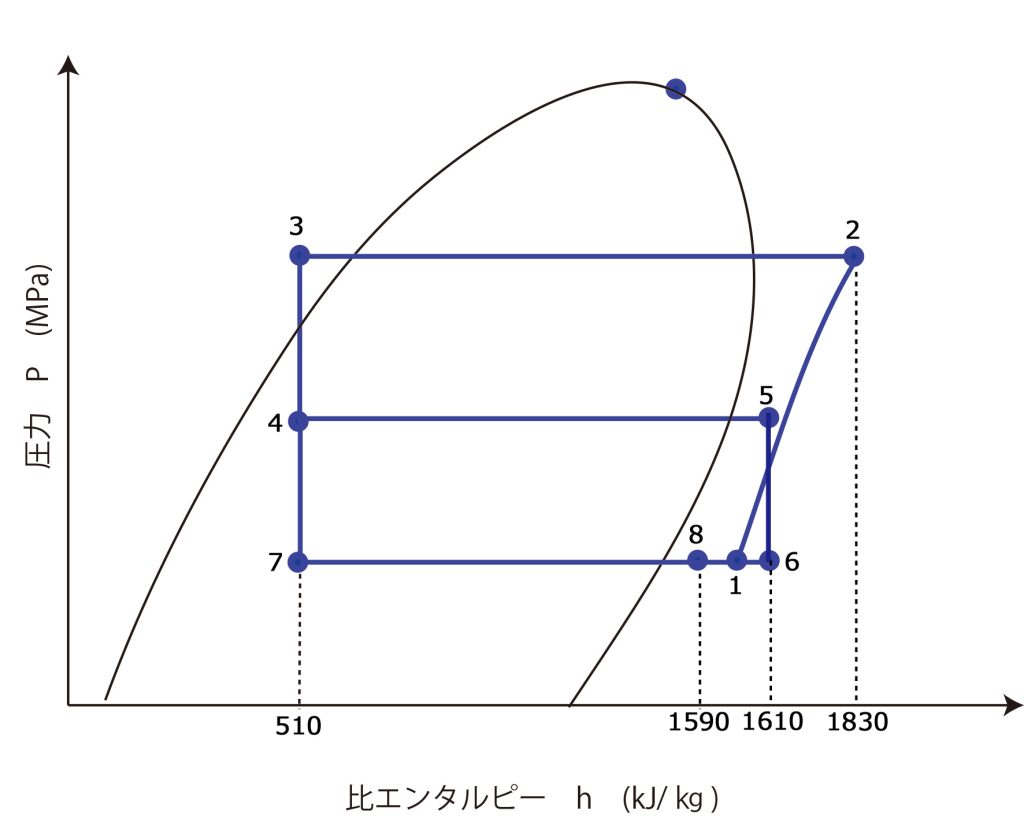
１．凝縮器を流れる実際の冷媒循環量$q_{mr}$(kg/sec)　は？

一般的に次の関係が成り立つ
冷媒循環量=$\frac{圧縮機の押しのけ量×体積効率}{圧縮機吸込み蒸気の比体積}$
この問題の場合は次のようになる（ただし、単位はm³/secに変換する）

$$q_{mr}=\frac{\frac{V}{3600}×η_{v}}{v_{1}}=\frac{\frac{360}{3600}×0.8}{0.4}=0.2　(kg/sec)$$

２．蒸発器Ⅰと蒸発器Ⅱの合計の実際の冷凍能力$Φ_{o}$（kW）　は？

冷凍能力$Φ_{o}$は蒸発器Ⅰの冷凍能力($Φ_{1}$)と蒸発器Ⅱの冷凍能力($Φ_{2}$)の合計である

$$Φ_{1}=q_{mr1}(h_{5}-h_{4})　　Φ_{2}=q_{mr2}(h_{8}-h_{7})$$

$q_{mr1}　：　q_{mr2}=１：１$　だから

$$Φ_{1}=\frac{q_{mr}}{2}(h_{5}-h_{4})　　Φ_{2}=\frac{q_{mr}}{2}(h_{8}-h_{7})$$

$Φ_{o}=Φ_{1}+Φ_{2}$だから(また、$h_{3}=h_{4}=h_{7}$)

$$Φ_{o}=\frac{q_{mr}(h_{5}+h_{8}-2×h_{3})}{2}=\frac{0.2×(1610+1590-2×510)}{2}=218 (kW)$$

この問題の解説は次の「上級冷凍受験テキスト」を参考にしました

上級冷凍受験テキスト第９次改訂/日本冷凍空調学会/日本冷凍空調学会

posted with カエレバ

楽天市場

Amazon

Yahooショッピング

３．圧縮機の実際の圧縮軸動力$P$（kW）は？

圧縮機動力　$P=q_{mr}×\frac{h_{2}-h_{1}}{η_{c}×η_{m}}$　　(A式)
圧縮機に入る前の熱バランスは　$q_{mr}・h_{1}=q_{mr1}・h_{6}+q_{mr2}×h_{8}$
$q_{mr1}=q_{mr2}=\frac{q_{mr}}{2}$　だから上の式は次のように変形できる
$h_{1}=\frac{h_{6}+h_{8}}{2}=\frac{h_{5}+h_{8}}{2}=1600$　(※　$h_{5}=h_{6}$だから)
後は上のA式に数値を代入すると

$$P=0.2×\frac{1830-1600}{0.7×0.9}≒73 (kW)$$

４．実勢の成績係数(COP)R　は？

$$(COP)R=\frac{Φ_{o}}{P}=\frac{218}{73}=1.1776≒2.99$$