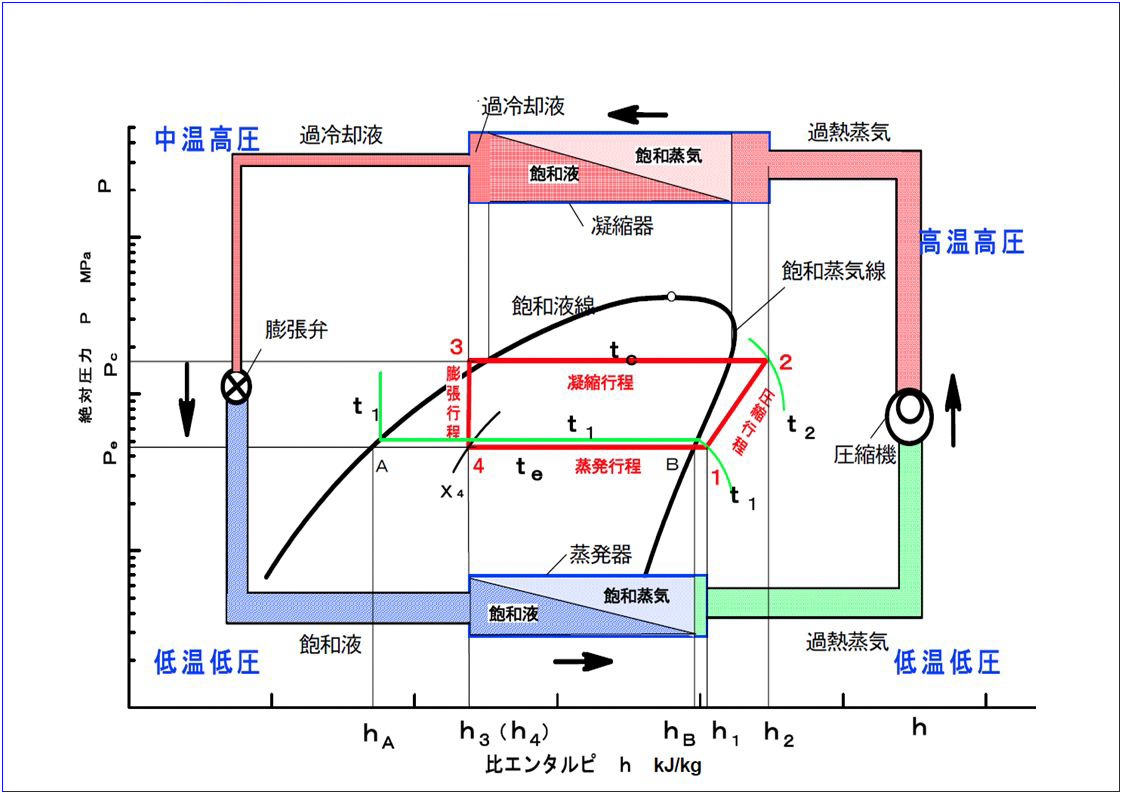
【問題】
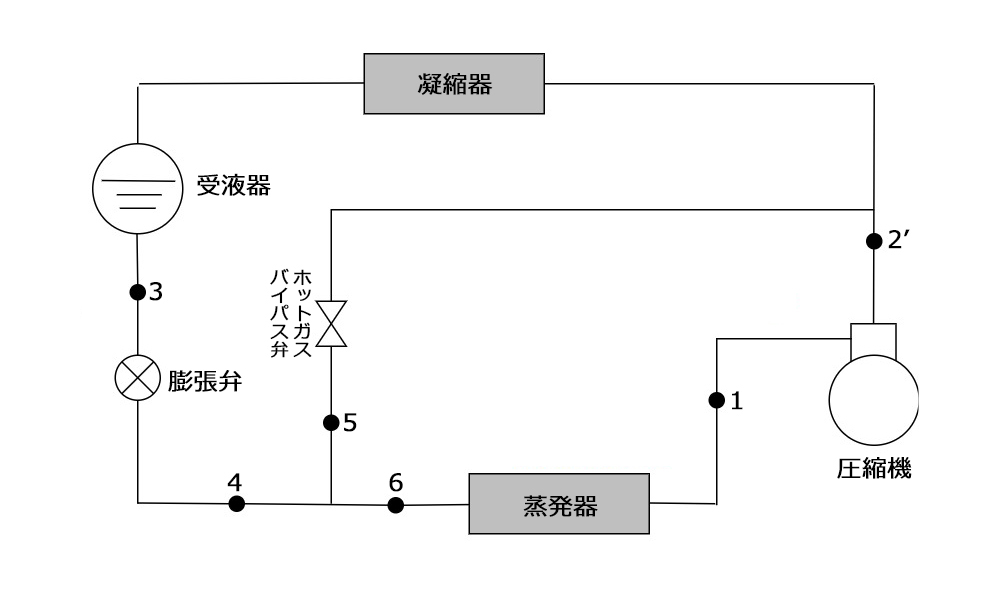
下図に示すR401A冷凍装置は、負荷減少時に圧縮機出口直後の吐出しガスの一部を蒸発器入口にバイパス弁を通して絞り膨張し容量制御を行っており、下記の条件で運転するものとする。
圧縮機の吐出しガス量の20%をバイパスをして容量制御を行っている。
ただし、圧縮機の機械的摩擦損失仕事は吐出しガスに熱として加わるものとする。また、配管での熱の出入りおよび圧力損失はないものとする。
| 【冷凍サイクルの運転条件】 | |
| 圧縮機の冷媒循環量 | \(q_{mr}\)=0.50 kg/sec |
| 圧縮機吸込み蒸気の比エンタルピー | \(h_{1}\)=421 kJ/㎏ |
| 圧縮機の断熱圧縮後の圧縮機吐出しガスの比エンタルピー | \(h_{2}\)=475 kJ/㎏ |
| 膨張弁直前の冷媒液の比エンタルピー | \(h_{3}\)=241 kJ/㎏ |
| 【圧縮機の効率】 | |
| 断熱効率 | \(η_{c}\)=0.70 |
| 機械効率 | \(η_{m}\)=0.85 |
1.バイパスされる冷媒蒸気の比エンタルピー\(h_{5}\)(kJ/kg) は?
2.容量制御時の冷凍能力\(Φ_{o}\)(kW) は?
3.容量制御時の成績係数は、全負荷時の何% は?
【解答】
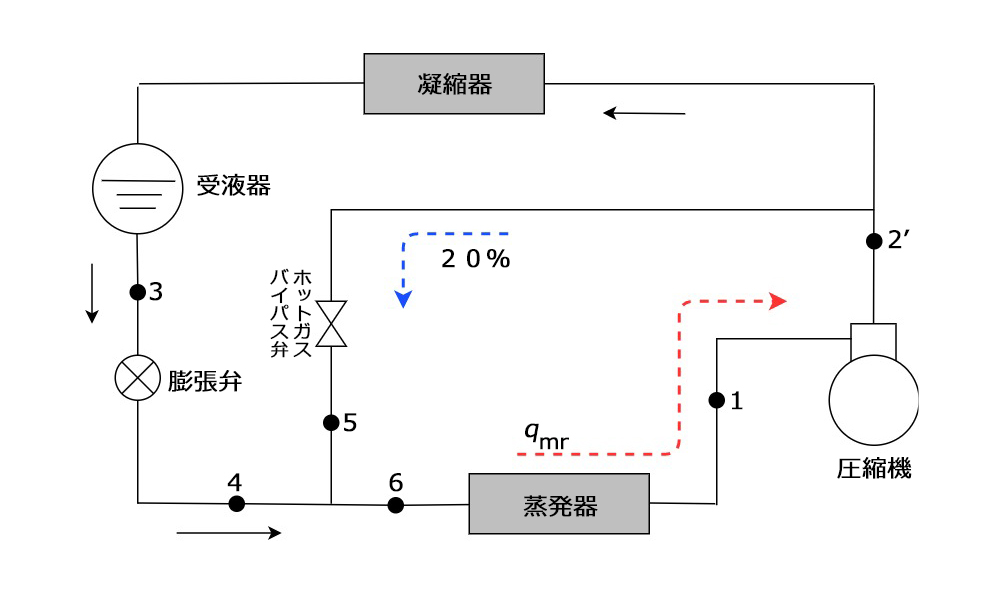
いつものように、p-h線図と冷媒の流れ概略図は次のように書く
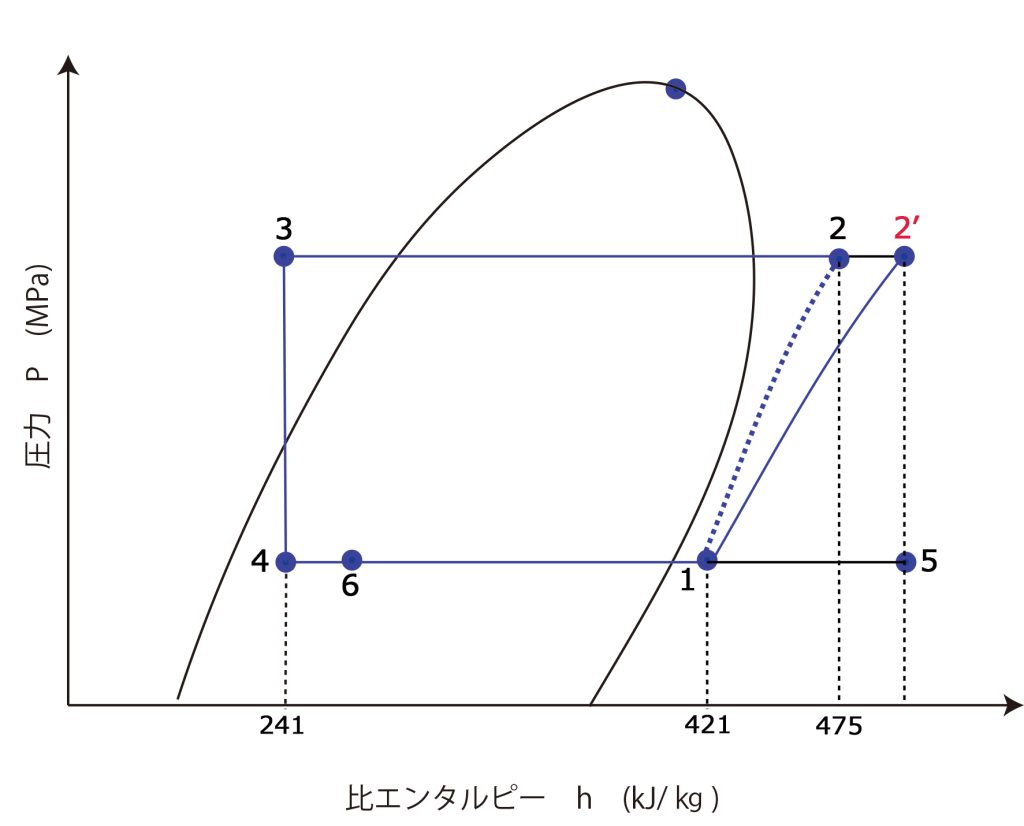
1.バイパスされる冷媒蒸気の比エンタルピー\(h_{5}\)(kJ/kg) は?
\(h_{5}=\color{red}{h’_{2}}\)なので\(\color{red}{h’_{2}}\)を求める
$$\color{red}{h’}_{\color{red}{2}}=h_{1}+\frac{h_{2}-h_{1}}{η_{c}・η_{m}}=421+\frac{475-421}{0.70×0.85}=511.756≒512 [kJ/kg]$$
2.容量制御時の冷凍能力\(Φ_{o}\)(kW) は?
$$Φ_{o}=q_{mr}(h_{1}-h_{6})$$
となるので\(h_{6}\)を求めれば良い
6では冷媒は\(q_{mr}\)流れ、5では0.2×\(q_{mr}\)流れ、4では0.8×\(q_{mr}\)流れており、熱収支を考えてみる。
$$q_{mr}・h_{6}=0.8・q_{mr}・h_{4}+0.2・q_{mr}・h_{5}$$
簡略化すると(\(h_{3}=h_{4}\) \(h_{5}\)は前問より512)
$$h_{6}=0.8・h_{4}+0.2・h_{5}=0.8×241+0.2×512=295.2≒295 [kJ/kg]$$
上の式に代入
$$Φ_{o}=q_{mr}(h_{1}-h_{6})=0.50×(421-295)=63 [kW]$$
この問題の解説は次の「上級冷凍受験テキスト」を参考にしました
3.容量制御時の成績係数は、全負荷時の何% は?
便宜上記号を次のように決める
| 全負荷時 | 容量制御時 | |
| 成績係数 | (COP)R | (COP)R’ |
| 冷凍能力 | $$Φ_{o}$$ | $$Φ’_{o}$$ |
$$(COP)R=\frac{Φ_{o}}{P} (COP)R’=\frac{Φ’_{o}}{P}$$
$$\frac{(COP)R’}{(COP)R}=\frac{\frac{Φ’_{o}}{P}}{\frac{Φ_{o}}{P}}=\frac{Φ’_{o}}{Φ_{o}}$$
ここで大事なことは
$$Φ_{o}=q_{mr}(h_{1}-h_{4}) Φ’_{o}=q_{mr}(h_{1}-h_{6})$$
なので(\(h_{6}\)は前問回答中295)
$$\frac{(COP)R’}{(COP)R}=\frac{Φ’_{o}}{Φ_{o}}=\frac{q_{mr}(h_{1}-h_{6})}{q_{mr}(h_{1}-h_{4})}=\frac{h_{1}-h_{6}}{h_{1}-h_{4}}=\frac{421-295}{421-241}=0.7$$
答え70%