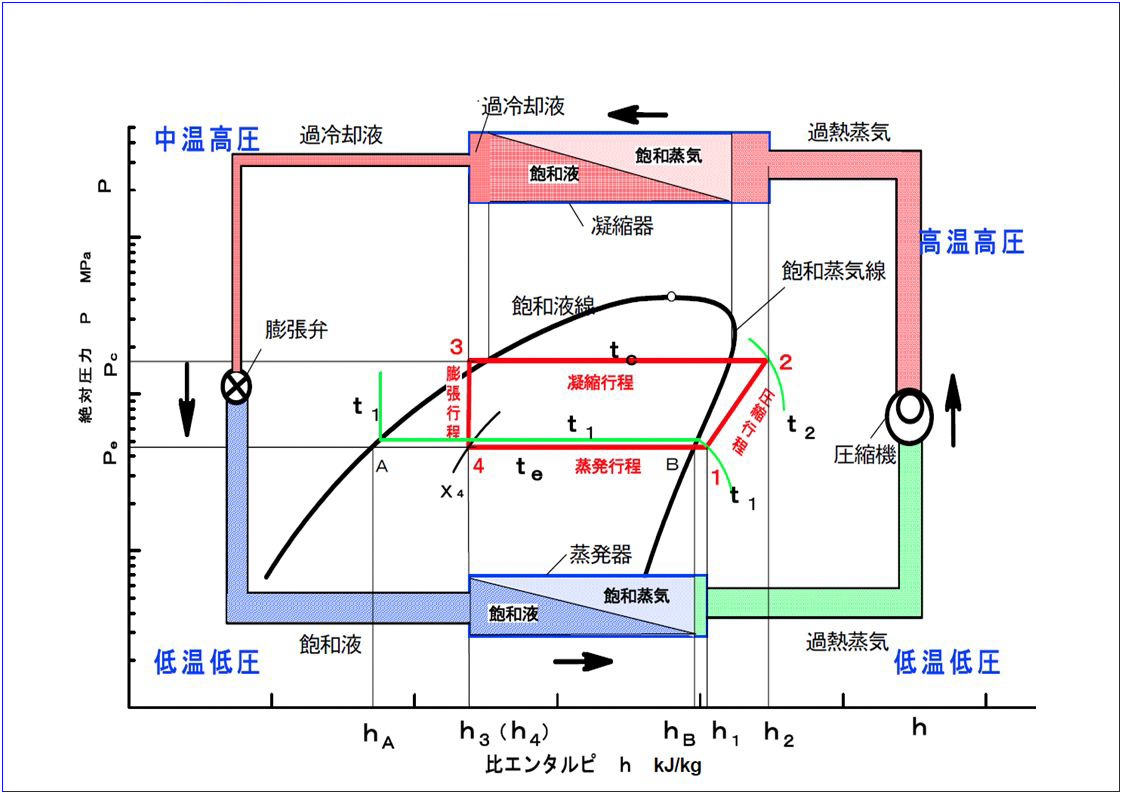
【問題】
R404Aを冷媒とする二段圧縮一段膨張の冷凍装置を、下記の冷凍サイクルの運転条件で運転する。
ただし、圧縮機の機械的摩擦損失仕事は吐き出しガスに熱として加わるものとする。また、配管での熱の出入りおよび圧力損失はないものとする。
| 【理論冷凍サイクルの運転条件】 | |
| 低段圧縮機吸込み蒸気の比エンタルピー | \(h_{1}\)=349 kJ/㎏ |
| 低段圧縮機の断熱圧縮後の吐出しガスの比エンタルピー | \(h_{2}\)=378 kJ/㎏ |
| 高段圧縮機吸込み蒸気の比エンタルピー | \(h_{3}\)=365 kJ/㎏ |
| 高段圧縮機の断熱圧縮後の吐出しガスの比エンタルピー | \(h_{4}\)=398 kJ/㎏ |
| 中間冷却器用膨張弁直前の液の比エンタルピー | \(h_{5}\)=254 kJ/㎏ |
| 蒸発器用膨張弁直前の液の比エンタルピー | \(h_{7}\)=200 kJ/㎏ |
| 【実際の運転条件】 | |
| 冷凍能力 | \(Φ_{m}=210\) kW |
| 断熱効率(低段側) | \(η_{cL}=0.70\) |
| 断熱効率(高段側) | \(η_{cH}=0.75\) |
| 機械効率(低段側、高段側とも) | \(η_{m}=0.90\) |
1.実際の中間冷却器へのバイパス冷媒循環量\(q’_{mL}\)(kg/sec)と低段側の冷媒循環量\(q_{mL}\)(kg/sec)との比(\(q’_{mL}/q_{mL})\)を求めよ。
2.実際の中間冷却器の必要冷却能力\(Φ_{m}\)(kW)を求めよ
3.実際の圧縮機駆動の総軸動力P(kW)を求めよ。
4.実際の冷凍装置の成績係数(COP)Rを求めよ。
【解答】
まず、p-h線図と機器相互の冷媒の流れ概略図を次のように書く
図 1
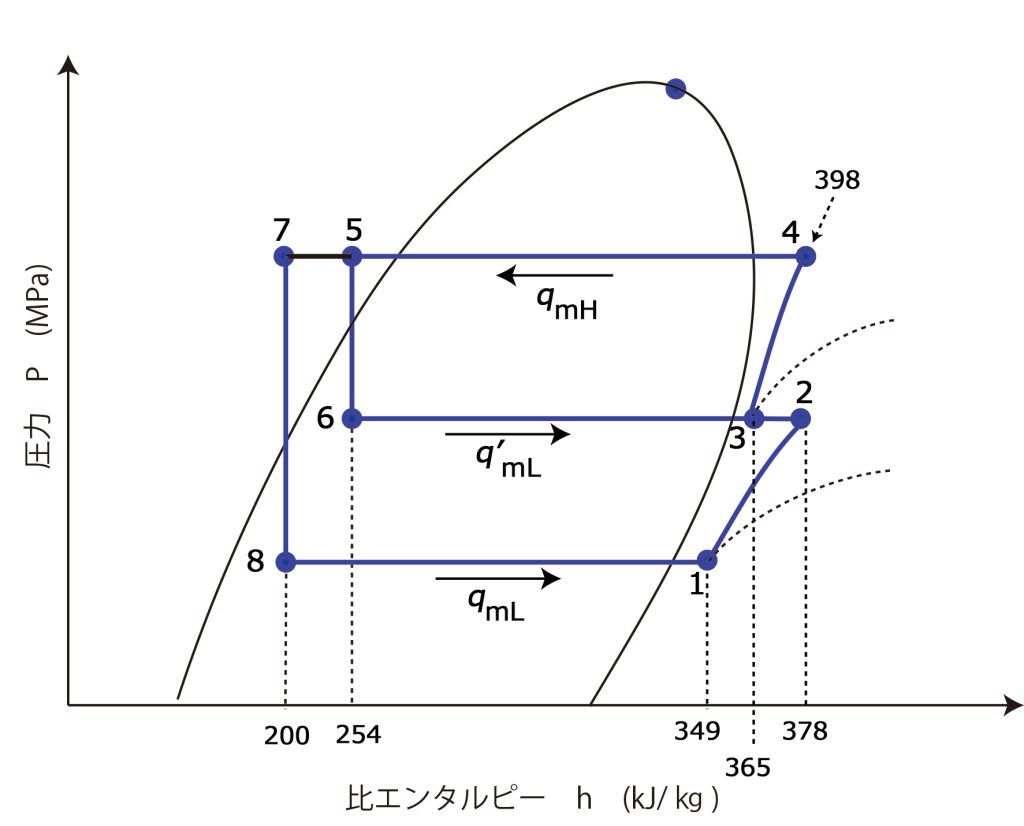
図 2
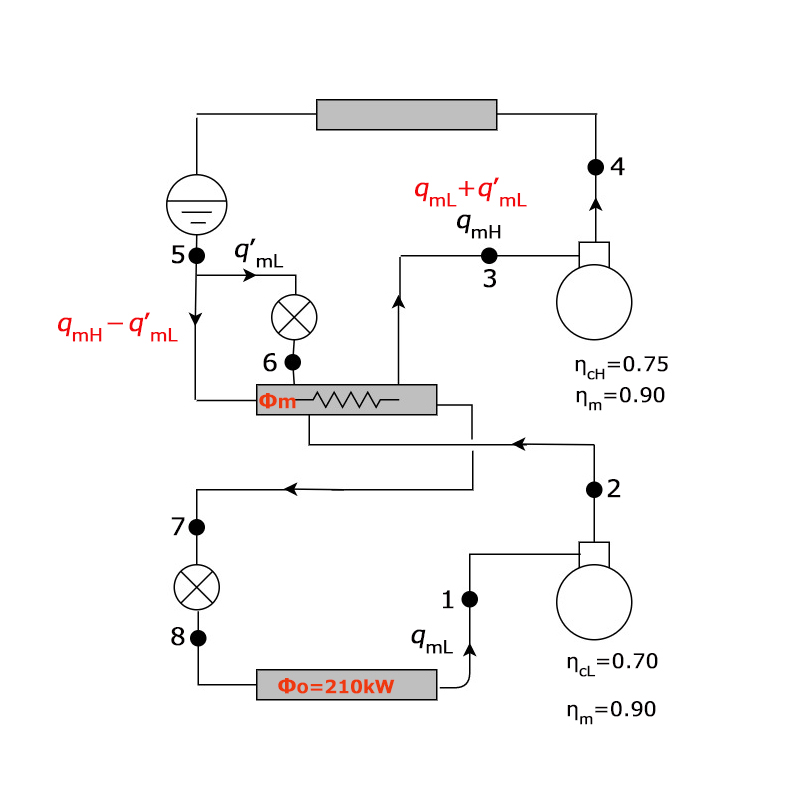
【解答】
1.実際の中間冷却器へのバイパス冷媒循環量\(q’_{mL}\)(kg/sec)と低段側の冷媒循環量\(q_{mL}\)(kg/sec)との比(\(q’_{mL}/q_{mL})\)を求めよ。
中間冷却器の熱収支を考える。
\(q_{mH}・h_{5}+q_{mL}・h’_{2}=q_{mH}・h_{3}+q_{mL}・h_{7}\) ただし、\(h_{2}\)ではなく\(h’_{2}\)である
さて、ここで\(h’_{2}\)を求める
図 3
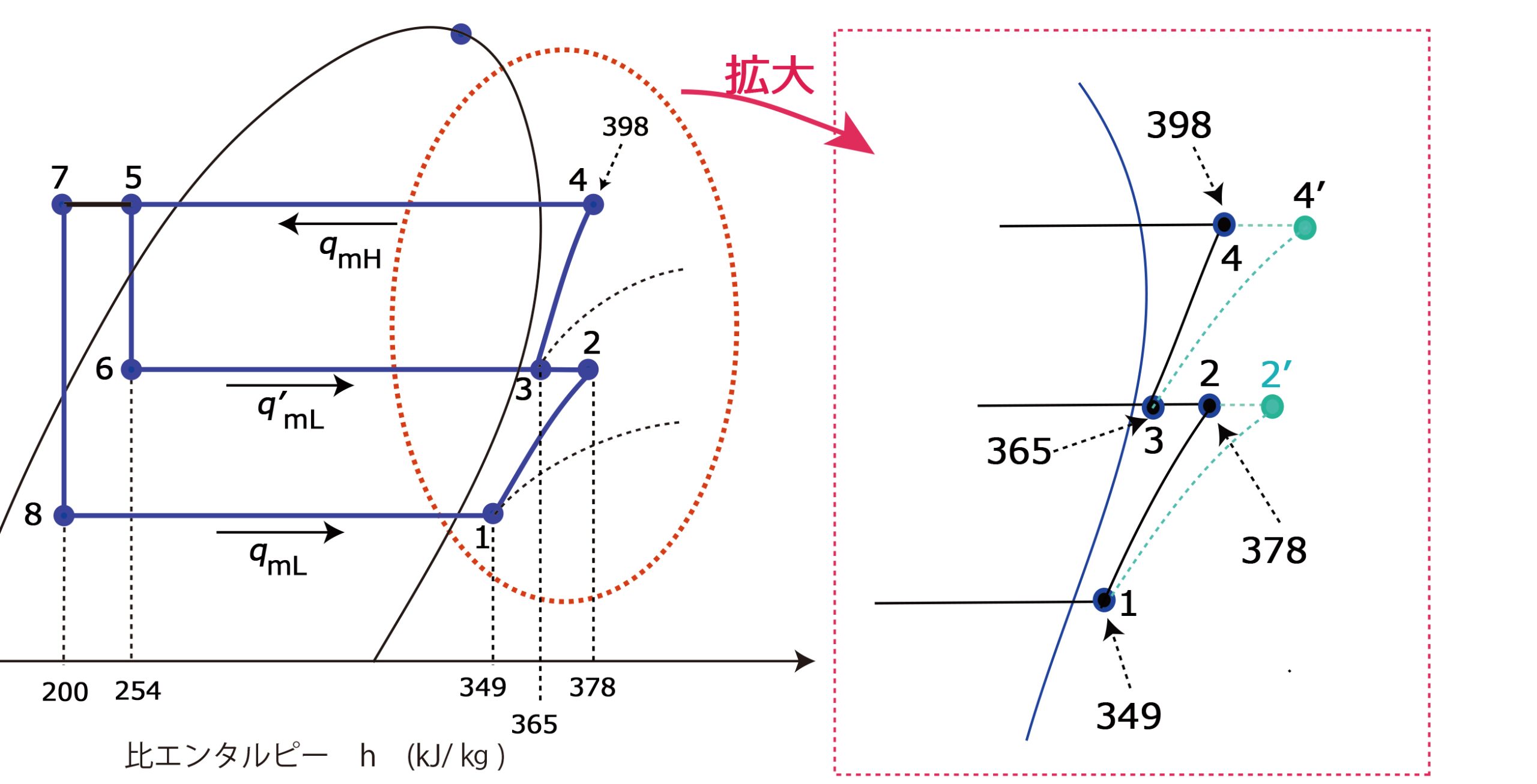
\(h’_{2}=h_{1}+\frac{\Large{h_{2}-h_{1}}}{\Large{η_{cL}・η_{m}}}=349+\frac{\Large{378-349}}{\Large{0.70・0.90}}=395.031≒395\)
\(q_{mH}・h_{5}+q_{mL}・h’_{2}=q_{mH}・h_{3}+q_{mL}・h_{7}\)を変形すると
\(q_{mL}・(h’_{2}-h_{7})=q_{mH}・(h_{3}-h_{5})\)
\(q_{mH}=q_{mL}+q’_{mL}\)だから
\(q_{mL}・((h’_{2}-h_{3})+(h_{5}-h_{7}))=q’_{mL}・(h_{3}-h_{5})\)
\(\frac{\Large{q’_{mL}}}{\Large{q_{mL}}}=\frac{\Large{(h’_{2}-h_{3})+(h_{5}-h_{7})}}{(\Large{h_{3}-h_{5})}}\)
数値を代入する。
\(\frac{\Large{q’_{mL}}}{\Large{q_{mL}}}=\frac{\Large{(395-365)+(254-200)}}{(\Large{365-254)}} \\
=0.7567≒0.757\)
2.実際の中間冷却器の必要冷却能力\(Φ_{m}\)(kW)を求めよ
中間冷却器に入るときの状態と出るときの状態は
| 冷媒循環量 | 入るとき | 出るとき | |
| \(q_{mL}\) | \(h_{5}\) | → → | \(h_{7}\) |
| \(q_{mL}\) | \(h’_{2}\) | → → | \(h_{3}\) |
よって中間冷却器の必要冷却能力\(Φ_{m}\)は
\(Φ_{m}=q_{mL}・((h_{5}-h_{7})+(h’_{2}-h_{3}))\)
\(Φ_{o}=q_{mL}・(h_{1}-h_{8})\)だから
\(q_{mL}=\frac{\Large{Φ_{o}}}{\Large{h_{1}-h_{8}}}=\frac{\Large{210}}{\Large{349-200}}=1.409≒1.41\)
\(Φ_{m}=q_{mL}・((h_{5}-h_{7})+(h’_{2}-h_{3}))=1.41・((254-200)+(395-365)) \\
=118.44≒118 kW\)
この問題の解説は次の「上級冷凍受験テキスト」を参考にしました
3.実際の圧縮機駆動の総軸動力P(kW)を求めよ。
低段側圧縮機駆動軸動力を\(P_{L}\)、高段側圧縮機駆動軸動力を\(P_{H}\)とする
圧縮機駆動の総軸動力 \(P=P_{L}+P_{H}\) となる
問1解答より \(h’_{2}-h_{1}=\frac{\Large{h_{2}-h_{1}}}{\Large{η_{cL}・η_{m}}}\)
また、\(h’_{4}-h_{3}=\frac{\Large{h_{4}-h_{3}}}{\Large{η_{cH}・η_{m}}}\)
\(P_{L}=q_{mL}・(h’_{2}-h_{1}) \\
P_{H}=q_{mH}・(h’_{4}-h_{3})\) だから
\(P=q_{mL}・\frac{\Large{h_{2}-h_{1}}}{\Large{η_{cL}・η_{m}}}+q_{mH}・\frac{\Large{h_{4}-h_{3}}}{\Large{η_{cH}・η_{m}}}\)
ここで \(q_{mH}\)を求めるには \(q_{mH}=q_{mL}+q’_{mL}\) に着目して、
問1解答より \(q’_{mL}=0.757・q_{mL}\)
問2回答中より \(q_{mL}=1.41\) だから
\(q_{mH}=1.757・1.41=2.477≒2.48\)kg/sec となる
さて、すべての数値が判明したのでいよいよ、数値を代入して\(P\)を求める
\(P=q_{mL}・\frac{\Large{h_{2}-h_{1}}}{\Large{η_{cL}・η_{m}}}+q_{mH}・\frac{\Large{h_{4}-h_{3}}}{\Large{η_{cH}・η_{m}}} \\
=1.41・\frac{\Large{378-349}}{\Large{0.70・0.90}}+2.48・\frac{\Large{398-365}}{\Large{0.75・0.90}} \\
=1.41・46.03+2.48・48.888=64.9023+121.24224=186.144≒186 kW\)
4.実際の冷凍装置の成績係数(COP)Rを求めよ。
この問題は簡単ですので式だけ示しておきます。ご自身で数値を代入してください
\((COP)R=\frac{\Large{Φ_{o}}}{\Large{P}}=\frac{\Large{210}}{\Large{186}}≒1.13\)
以上で終わり