【問題】
R404Aコンパウンド圧縮機を使用した二段圧縮一段膨張冷凍装置を、下記の冷凍サイクルの条件で運転する。
ただし、圧縮機の機械的摩擦損失は吐出しガスに熱として加わらないものとする。また、配管での熱の出入りはないものとする。
| 【冷凍サイクルの運転条件】 | |
| 低段圧縮機吸込み蒸気の比エンタルピー | \(h_{1}\)=352 kJ/㎏ |
| 低段圧縮機吸込み蒸気の比体積 | \(v_{1}\)=0.19 m3/㎏ |
| 低段圧縮機断熱圧縮後の吐出しガスの比エンタルピー | \(h_{2}\)=381 kJ/㎏ |
| 高段圧縮機吸込み蒸気の比エンタルピー | \(h_{3}\)=369 kJ/㎏ |
| 高段圧縮機吸込み蒸気の比体積 | \(v_{3}\)=0.045 m3/㎏ |
| 高段圧縮機断熱圧縮後の吐出しガスの比エンタルピー | \(h_{4}\)=404 kJ/㎏ |
| 中間冷却器用膨張弁直前の液の比エンタルピー | \(h_{5}\)=268 kJ/㎏ |
| 蒸発器用膨張弁直前の液の比エンタルピー | \(h_{7}\)=248 kJ/㎏ |
| 【圧縮機の効率】 | |
| 体積効率(低段側、高段側とも) | \(η_{v}\)=075 |
| 断熱効率(低段側、高段側とも) | \(η_{c}\)=0.73 |
| 機械効率(低段側、高段側とも) | \(η_{m}\)=0.90 |
1.低段側と高段側との気筒数比がいくらのコンパウンド圧縮機を選定したらよいか。 ?
2.実勢の成績係数(COP)R は?
ただし、
低段圧縮機のピストン押しのけ量 \(V_{L}\) (m3/sec)
高段圧縮機のピストン押しのけ量 \(V_{H}\) (m3/sec)
低段側の冷媒循環量 \(q_{mL}\) (kg/sec)
高段側の冷媒循環量 \(q_{mH}\) (kg/sec)
【解答】
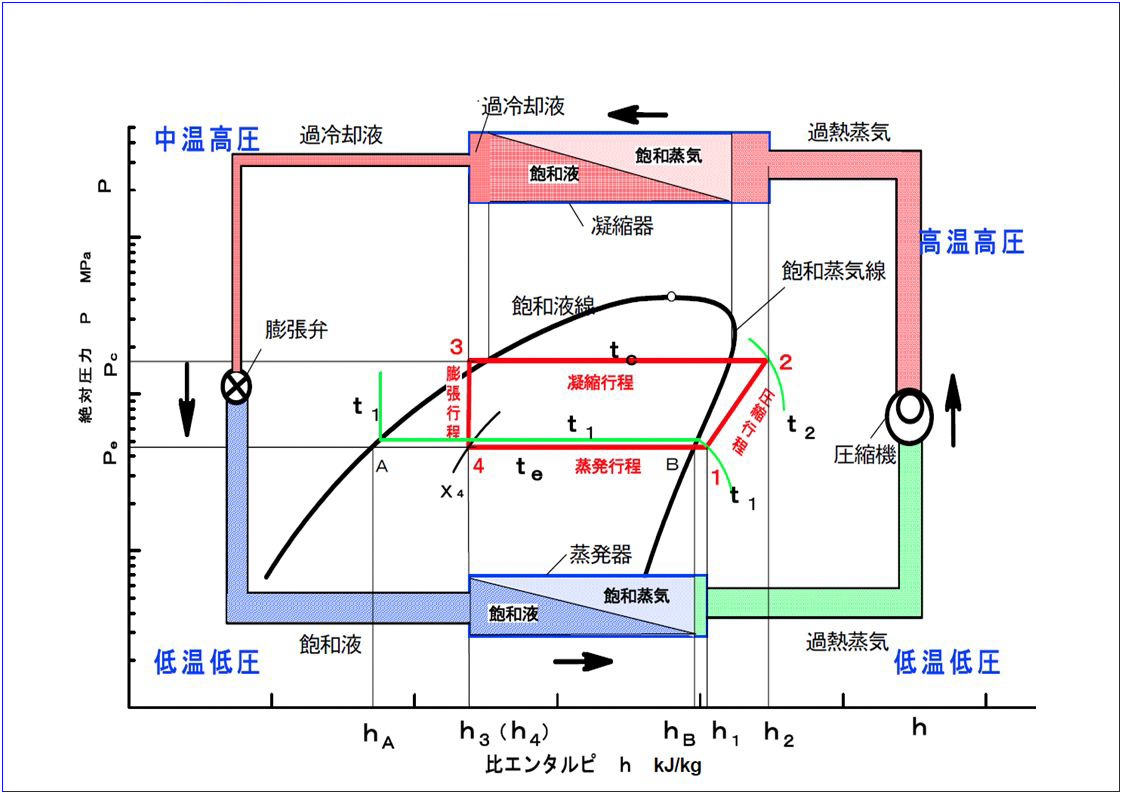
いつものように、p-h線図と冷媒の流れ概略図は次のようになる
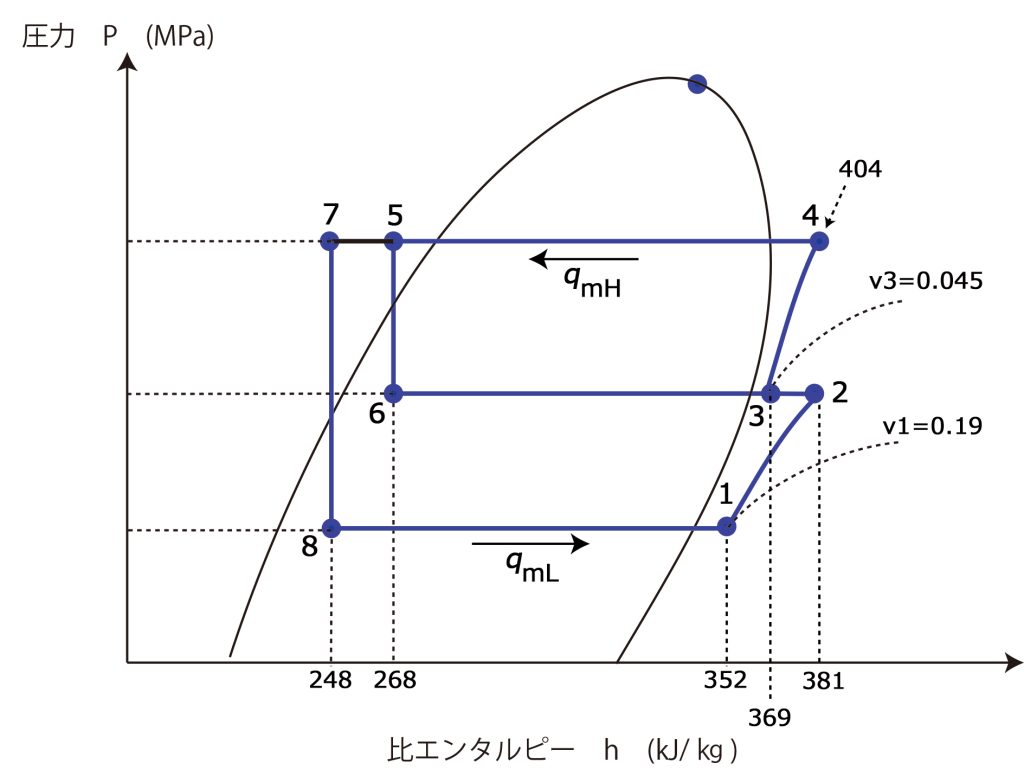
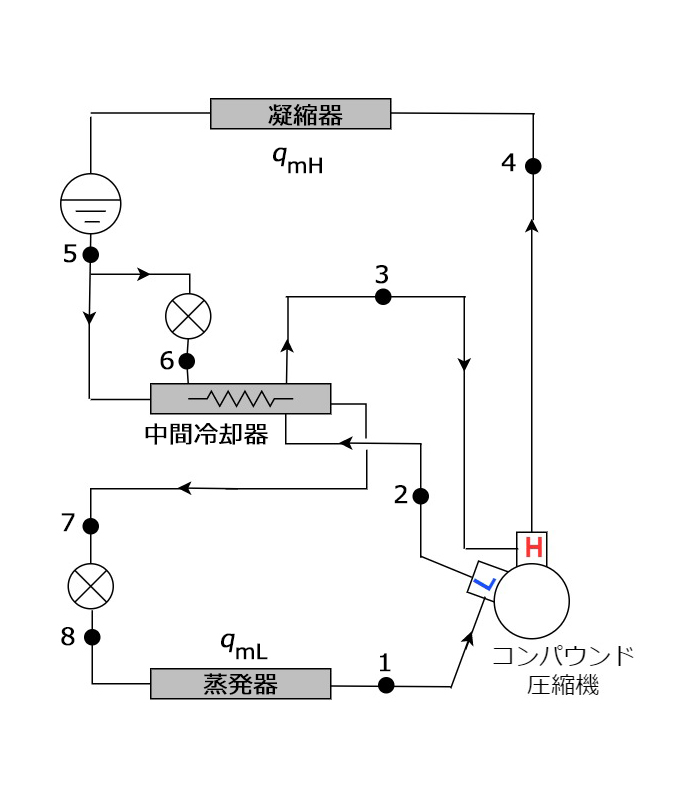
1.低段側と高段側との気筒数比がいくらのコンパウンド圧縮機を選定したらよいか。 ?
一般的にピストン押しのけ量(\(V\))、冷媒循環量(\(q\))、体積効率( \(η_{v}\))、比体積(\(v\))の関係式は
\(V\)×\(η_{v}\)=\(q\)×\(v\) だから
$$V_{L}=\frac{q_{mL}×v_{1}}{η_{v}} V_{H}=\frac{q_{mH}×v_{3}}{η_{v}} $$
さて、気筒数比(r)はピストン押しのけ量比と同等ですから次のようになります
$$r=\frac{V_{L}}{V_{H}}=\frac{\frac{q_{mL}×v_{1}}{η_{v}}}{\frac{q_{mH}×v_{3}}{η_{v}}}=\frac{q_{mL}×v_{1}}{q_{mH}×v_{3}} A式$$
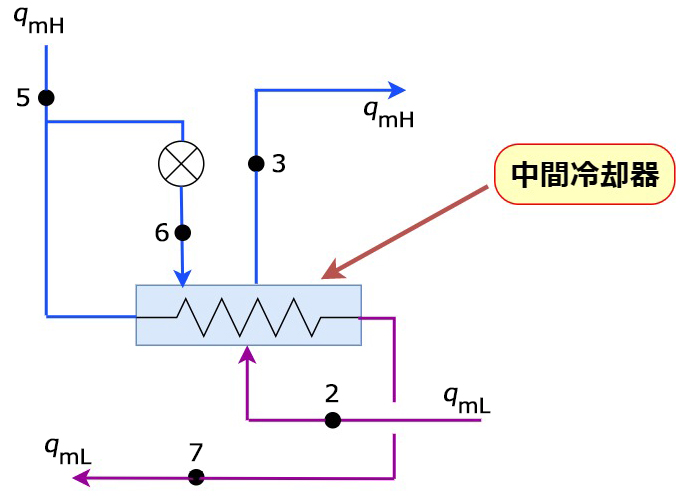
そこで、\(q_{mL}\)と\(q_{mH}\)の関係はどうなっているでしょうか、それをみるには中間冷却器の熱収支を見ます
中間冷却器に入る熱=中間冷却器から出る熱(ただし、\(h_{2}\)ではなく\(h’_{2}\)を使う)
$$q_{mH}・h_{5}+q_{mL}・h’_{2}=q_{mH}・h_{3}+q_{mL}・h_{7}$$
変形すると
$$q_{mL}(h’_{2}-h_{7})=q_{mH}(h_{3}-h_{5}) \frac{q_{mL}}{q_{mH}}=\frac{h_{3}-h_{5}}{h’_{2}-h_{7}}$$
次に\(h’_{2}\)を求めますが、問題の条件として「圧縮機の機械的摩擦損失は吐出しガスに熱として加わらないものとする」となっていますので機械効率は無視し、断熱効率だけを考慮します
$$h’_{2}=h_{1}+\frac{h_{2}-h_{1}}{η_{c}}=352+\frac{381-352}{0.73}=391.7260≒391.7 [kJ/kg]$$
\(h’_{2}\)が判りましたのでA式に代入します
$$r=\frac{q_{mL}×v_{1}}{q_{mH}×v_{3}}=\frac{v_{1}}{v_{3}}×\frac{h_{3}-h_{5}}{h’_{2}-h_{7}}=\frac{0.19}{0.045}×\frac{369-268}{391.7-248}≒2.97$$
故に気筒数比が3のコンパウンド圧縮機
この問題の解説は次の「上級冷凍受験テキスト」を参考にしました
2.実勢の成績係数(COP)R は?
成績係数の基本公式は
$$(COP)R=\frac{Φ_{o}}{P} Φ_{o}=q_{mL}×(h_{1}-h_{8}) P=P_{L}+P_{H}$$
$$P_{L}=\frac{q_{mL}(h_{2}-h_{1})}{η_{c}・η_{m}} P_{H}=\frac{q_{mH}(h_{4}-h_{3})}{η_{c}・η_{m}}$$
$$P=\frac{q_{mL}(h_{2}-h_{1})}{η_{c}・η_{m}}+\frac{q_{mH}(h_{4}-h_{3})}{η_{c}・η_{m}} B式$$
前問の解答から
$$q_{mL}(h’_{2}-h_{7})=q_{mH}(h_{3}-h_{5}) q_{mH}=\frac{q_{mL}(h’_{2}-h_{7})}{h_{3}-h_{5}}$$
B式の\(q_{mH}\)に代入すると
$$P=\frac{q_{mL}(h_{2}-h_{1})}{η_{c}・η_{m}}+\frac{\frac{q_{mL}(h’_{2}-h_{7})}{h_{3}-h_{5}}(h_{4}-h_{3})}{η_{c}・η_{m}}$$
さて、(COP)Rの基本公式に代入すると
$$(COP)R=\frac{Φ_{o}}{P}=\frac{q_{mL}×(h_{1}-h_{8})}{\frac{q_{mL}(h_{2}-h_{1})}{η_{c}・η_{m}}+\frac{\frac{q_{mL}(h’_{2}-h_{7})}{h_{3}-h_{5}}(h_{4}-h_{3})}{η_{c}・η_{m}}}$$
整理すると
$$(COP)R=\frac{Φ_{o}}{P}=\frac{(h_{1}-h_{8})}{\frac{(h_{2}-h_{1})}{η_{c}・η_{m}}+\frac{\frac{(h’_{2}-h_{7})}{h_{3}-h_{5}}(h_{4}-h_{3})}{η_{c}・η_{m}}}$$
あとは適宜見やすいように変形してもよし、このまま数値を代入してもよし、結果を記すと
(COP)R=0.87
お疲れ様でした
何はともあれ、やはり下図の中間冷却器の熱収支が大事です