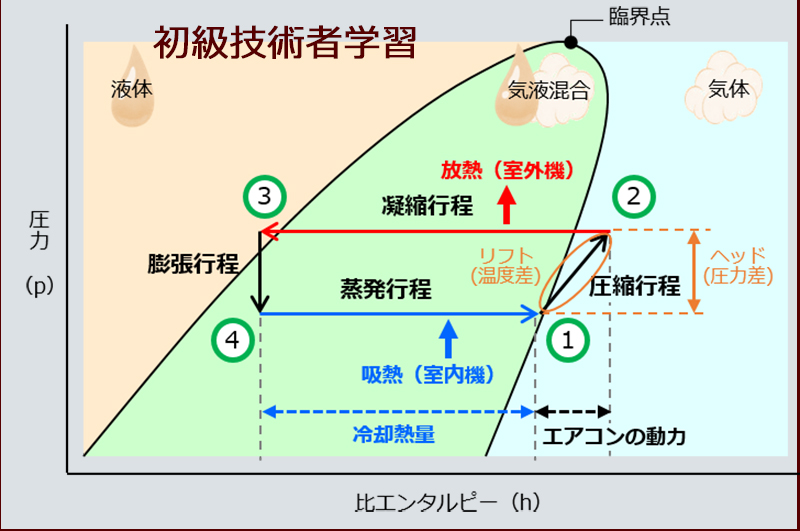
[問題] R404A冷凍装置が下記の条件で運転されている。このとき、冷媒循環量\(q_{mr}\)と実際の成績係数\((COP)_{R}\)を求めよ。
ただし、圧縮機の機械的摩擦損失仕事は吐出しガスに熱として加わるものとする。また、配管での熱の出入りおよび圧力損失はないものとする。
(運転条件)
圧縮機のピストン押しのけ量 \(V=250m^{3}/h\)
圧縮機の吸込み蒸気の密度 \(ρ=10kg/m^{3}\)
圧縮機吸込み蒸気の比エンタルピー \(h_{1}=360kJ/kg\)
断熱圧縮後の吐出しガスの比エンタルピー \(h_{2}=400kJ/kg\)
蒸発器入口冷媒の比エンタルピー \(h_{4}=230kJ/kg\)
圧縮機の体積効率 \(η_{v}=0.70\)
圧縮機の断熱効率 \(η_{c}=0.80\)
圧縮機の機械効率 \(η_{m}=0.90\)
[解答]
上記条件でのP-h線図は次のようになる
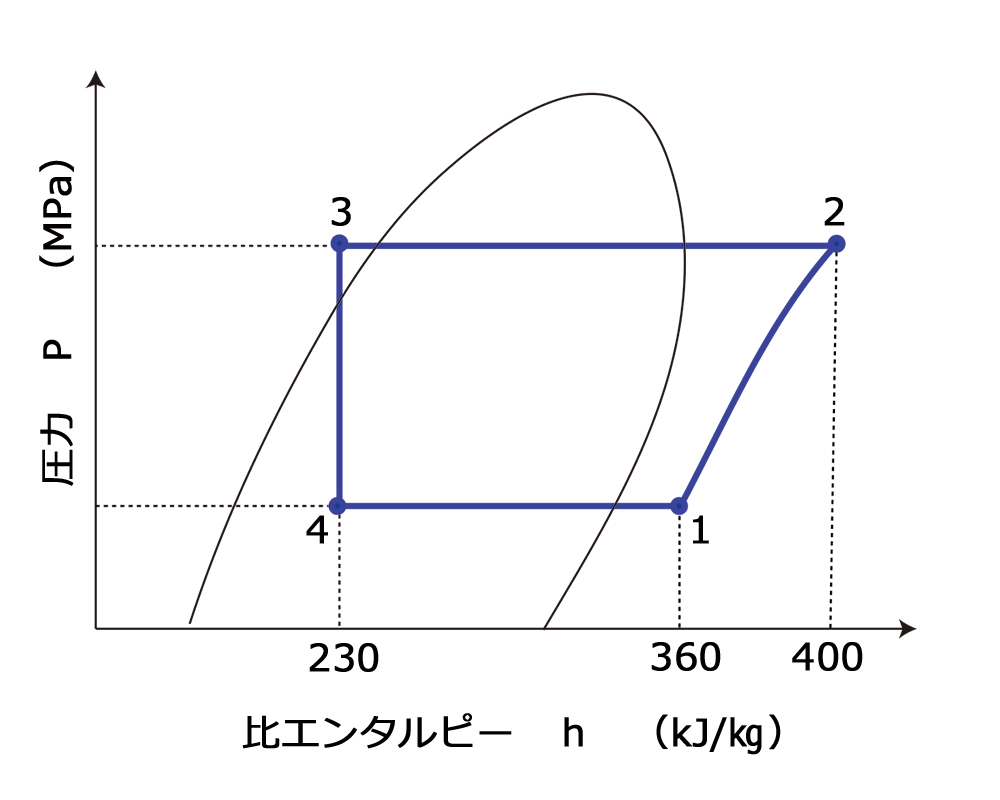
●冷媒循環量を求めるには次の公式を利用する
\(V・η_{v}=q_{mr}・v\) \(v\) 比体積 式A
問題では比体積ではなく密度が指定されているが、密度と比体積はそれぞれ逆数の関係にあるので
比体積\(v\)は \(v=\Large{\frac{1}{密度ρ}}\)となる
式Aを変換して冷媒循環量\(q_{mr}\)は
\(q_{mr}=\Large{\frac{V・η_{v}}{\frac{1}{ρ}}}\)\(=V・η_{v}・ρ\)
ここで、ピストン押しのけ量は、\(250m^{3}/h\) と1時間あたりになっているので、秒あたりにに換算すると
\(q_{mr}=\frac{\Large{V・η_{v}・ρ}}{\Large{3600}}\) となる この式に問題の数値を代入する
\(q_{mr}=\frac{\Large{250×0.7×10}}{\Large{3600}}=0.486111≒0.486(Kg/s)\)
●成績係数\((COP)_{R}\)を求める
次の公式を必ず覚えるとよい
\((COP)_{R}=\frac{\Large{h_{1}-h_{4}}}{\Large{h_{2}-h_{1}}}・η_{c}・η_{m}\) 式B
式Bに数値を代入すると
\((COP)_{R}=\frac{\Large{360-230}}{\Large{400-360}}・0.8・0.9\)=2.34
参考にしたテキスト ↓