【問題】下記の仕様で、屋外に設置して凝縮温度50℃で運転されるR410A冷凍装置の高圧受液器(円筒胴圧力容器)を製作したい。この高圧受液器について、次の(1)の問に答えよ。また、(2)および(3)の問に、計算式を示して答えよ。
ただし、R410Aの凝縮温度50℃における高圧部設計圧力は2.96MPaとする。
仕様;
使用鋼板
円筒胴の内径
円筒胴の腐れしろ
円筒胴板の溶接継手の効率
SM400B
\(D_{i}=380 ㎜\)
\(α=1 ㎜\)
\(η=0.70\)
(1) 使用鋼板の許容引張応力\(σ_{a} (N/mm^{2})\)の値の求め方は?
(2) この受液器の円筒銅板の必要厚さ\(t_{a}(㎜)\)の整数値は?
(3) この受液器に設計圧力の1.5倍の圧力\(P_{t}(MPa)\)が加わったとき、円筒銅板に誘起される接線方向の引張応力\(σ_{t}(N/mm^{2})\)を求めよ。
なお、この受液器の円筒銅板の厚さは、(2)で求めた必要厚さとする。
【解答】
(1) 使用鋼板の許容引張応力\(σ_{a} (N/mm^{2})\)の値の求め方は?

さて、ここで使用鋼板SM400Bの表記についておさらいです
SM400BのS は鋼 Mは船舶用の頭文字
SM400Bの400は 最小引張強さが\(400N/mm^{2}\)であることを示している
SM400BのBは炭素含有量の程度を示し、A > B > Cの順に炭素含有量が少なくなる
さて、常温での許容引張応力\(σ_{a} \)は最小引張強さの1/4であるので\(100 N/㎜^{2}\)となる
(2) この受液器の円筒銅板の必要厚さ\(t_{a}(㎜)\)の整数値は?
最小必要板厚計算の次の基本式に数値を代入して
\(t_{a}=\frac{\Large{PD_{i}}}{\Large{2σ_{a}η-1.2P}} +α\)
\(t_{a}=\frac{\Large{2.96・380}}{\Large{2・100・0.7-1.2・2.96}} +1=9.2434\)
最小必要板厚は大きめにとるため数値を切り上げて10㎜となる
(3) この受液器に設計圧力の1.5倍の圧力\(P_{t}(MPa)\)が加わったとき、円筒銅板に誘起される接線方向の引張応力\(σ_{t}(N/mm^{2})\)を求めよ。
なお、この受液器の円筒銅板の厚さは、(2)で求めた必要厚さとする。
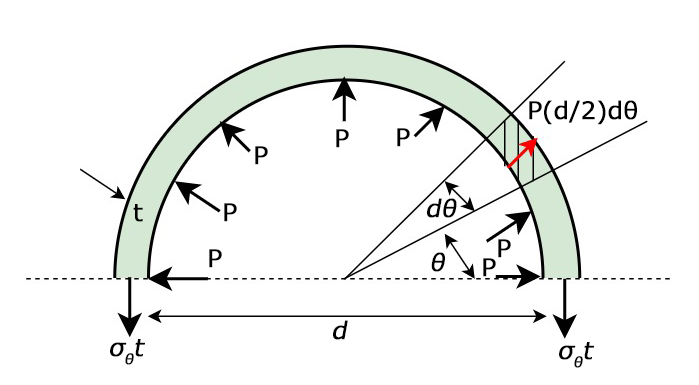
銅板に誘起される最大引張応力は円筒胴の接線方向の応力\(σ_{t}\)の基本式は次の通り、
\(σ_{t}=\frac{\Large{PD_{i}}}{\Large{2t_{a}}}\)
設計圧力と許容圧力
設計圧力どおり製作されたもので、腐食などがないことが確認されたものは、許容圧力の計算(板厚からの逆算など)をすることなく、設計圧力を許容圧力としてよい。
上記より設計どおりに制作されたと確認されたものは、設計圧力を許容圧力としてもよいので、最小試験圧力\(P_{t}\)は、
\(P_{t}=1.5P=1.5×2.96=4.44MPa\)
以上から\(P_{t}\)で生じる引張応力は
\(σ_{t}=\frac{\Large{P_{t}D_{i}}}{\Large{2t_{a}}}=\frac{\Large{4.44×380}}{\Large{2×10}}=84.36≒84.4\)
次のテキストを参考にする方が良い