熱伝導について
1.熱伝導
1.1 熱流束
単位時間 [sec]に単位面積 [m2]当たりを通過する熱量 [J]を熱流束 [W/m2]と言う。
一般に,熱が伝わる物体(物質)の断面積が変化するため,熱流束は次の微分形で表わされる。
$$q=\frac{dQ}{dA} [W/m^{2}]$$
\(Q\) は単位時間当たりの通過熱量(伝熱量)[J/sec],\(A\) は断面積 [m2]。
通過熱量(断面を通過する熱量,伝熱量ともいう)は熱流束を断面積で積分したものとなり,次式で表される。
$$Q=\int qdA\\$$
断面積が一定の場合,どの断面でも通過熱量(伝熱量)は等しい.同様に,熱流束もどの断面でも等しくなる.熱流束\(q\) を,断面積を\(A\) とすると通過熱量\(Q\) は
$$Q=\int qdA=q\int dA=qA$$
1.2 フーリエの法則
フーリエの法則とは,通過熱量(伝熱量)は温度勾配に比例するという法則であり次の式である(\(dQ\):単位時間に面積\(dA\) を通過する熱量、λ:熱伝導率、\(dθ/dx\):温度勾配)
$$dQ=-λ\frac{dθ}{dx}dA$$
熱流束に変形すると
$$q=\frac{dQ}{dA}=\frac{-λ\frac{dθ}{dx}dA}{dA}=-λ\frac{dθ}{dx} (A式)$$
1.3 熱伝導率,\(λ\)
熱伝導率\(λ\) [W/(mK)]とはその材質の熱の伝わりやすさを示す値であり,物質の種類によって固有の値を持ち,熱伝導率の値は,金属>液体>気体 の順となる。
1.4 単一平板の熱伝導
熱流速に対するフーリエの式(A式)を変形すると
$$dθ=-\frac{q}{λ}dx$$
これを積分すると
$$\int dθ=-\int \frac{q}{λ}dx$$
$$\int dθ=θ だから θ=-\frac{q}{λ}\int dx=-\frac{q}{λ}(x+C) =-\frac{q}{λ}x+C’ (C、C’は定数)$$
これを図に表すと下図のように温度変化は赤い直線となる

$$x=0 で θ=θ_{1} だから$$
$$θ_{1}=-\frac{q}{λ}x+C’=0+C’ θ_{1}=C’ だから$$
$$θ=-\frac{q}{λ}x+θ_{1}$$
$$x=L で θ=θ_{2} だから$$
$$θ_{2}=-\frac{q}{λ}L+θ_{1}$$
$$q=\frac{λ}{L}(θ_{1}-θ_{2})$$
この結果熱流束は熱伝導率と温度差に比例し、板の厚さに反比例する
2.熱通過
2.1 熱伝達率
流体から壁面もしくはその逆で壁面から流体に熱が伝わる場合の熱伝達の基本式
\(Q=h・A・(θ_{r}-θ_{w})\) \(h\):熱伝達率、\(A\):伝熱面積、\(θ_{r}\):流体の温度、\(θ_{w}\):壁の温度
2.2 壁を挟んでの熱通過
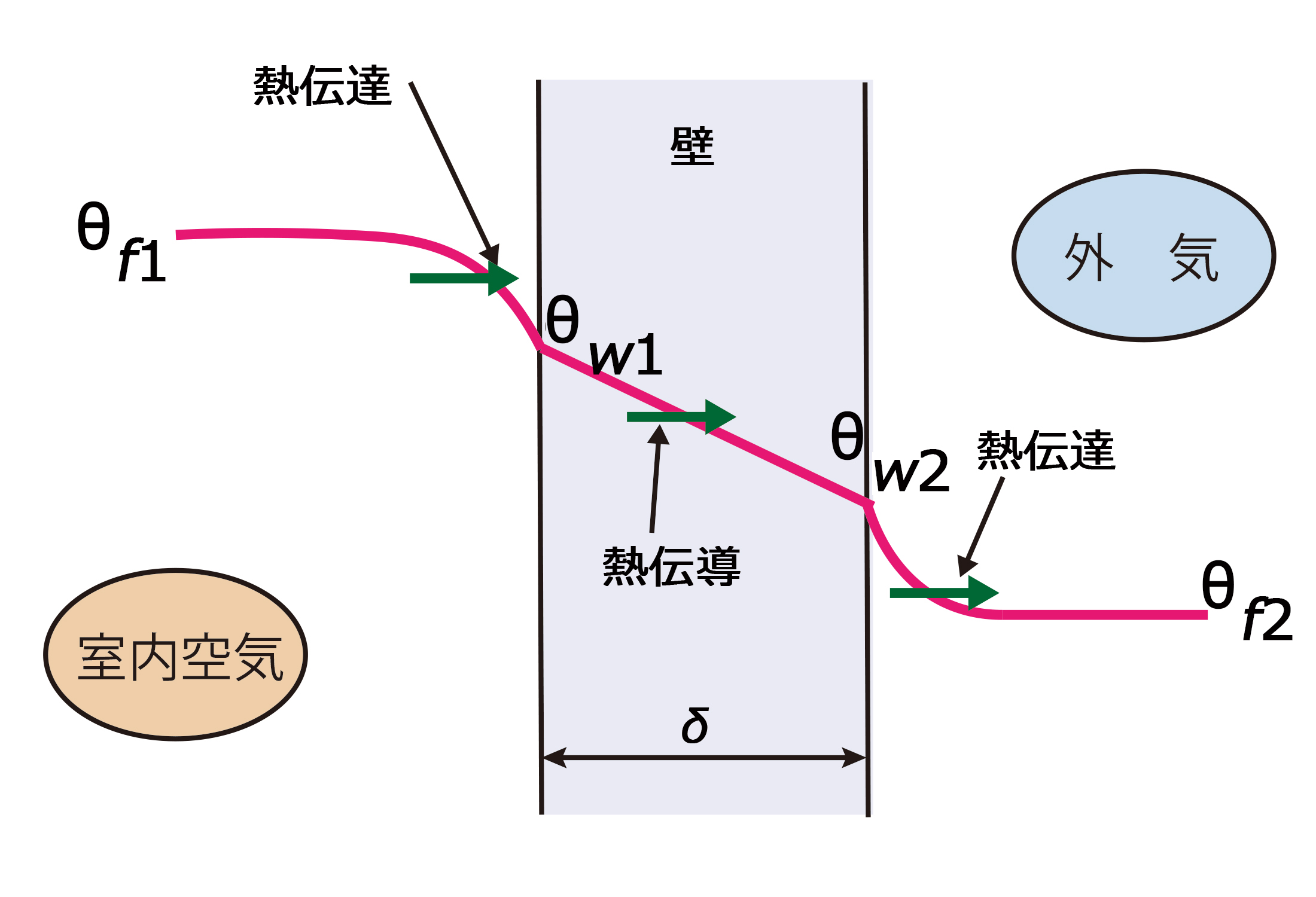
壁をはさんで,流体から別の流体に熱が移動する伝熱形式は,熱通過と呼ばれる。今は話をわかりやすくするため、冬場の暖房時において室内から外気に流れる熱量を考える。

上図のように、室内から壁へは熱伝達,壁内部は熱伝導,壁から外気は熱伝達が行われ,しかもそれらは同時に行われている。この場合次の基本式が成り立つ。(\(h_{1},h_{2}\)は熱伝達率、\(λ\)は熱伝導率 \(q_{1},q_{2}.q_{3}\)は移動する熱量)
室内熱伝達: \(q_{1}=h_{1}(θ_{f1}-θ_{w1})\)
壁内部熱伝導: \(q_{2}=\frac{λ}{δ}(θ_{w1}-θ_{w2})\)
外気熱伝達: \(q_{3}=h_{2}(θ_{w2}-θ_{f2})\)
変形すると
$$θ_{f1}-θ_{w1}=\frac{q_{1}}{h_{1}}$$
$$θ_{w1}-θ_{w2}==\frac{δ}{λ}q_{2}$$
$$θ_{w2}-θ_{f2}=\frac{q_{3}}{h_{2}}$$
上記3式右辺左辺合計すると
$$θ_{f1}-θ_{f2}=\frac{q_{1}}{h_{1}}+\frac{δ}{λ}q_{2}+\frac{q_{3}}{h_{2}}$$
理論的には\(q_{1}=q_{2}=q_{3}\)だからこれを\(q\)とすると
$$θ_{f1}-θ_{f2}=q(\frac{1}{h_{1}}+\frac{δ}{λ}+\frac{1}{h_{2}})$$ $$q=\frac{1}{\frac{1}{h_{1}}+\frac{δ}{λ}+\frac{1}{h_{2}}}(θ_{f1}-θ_{f2})$$
上記式の
$$k=\frac{1}{\frac{1}{h_{1}}+\frac{δ}{λ}+\frac{1}{h_{2}}} [W/(m^{2}・K)]$$
を熱通過率という
