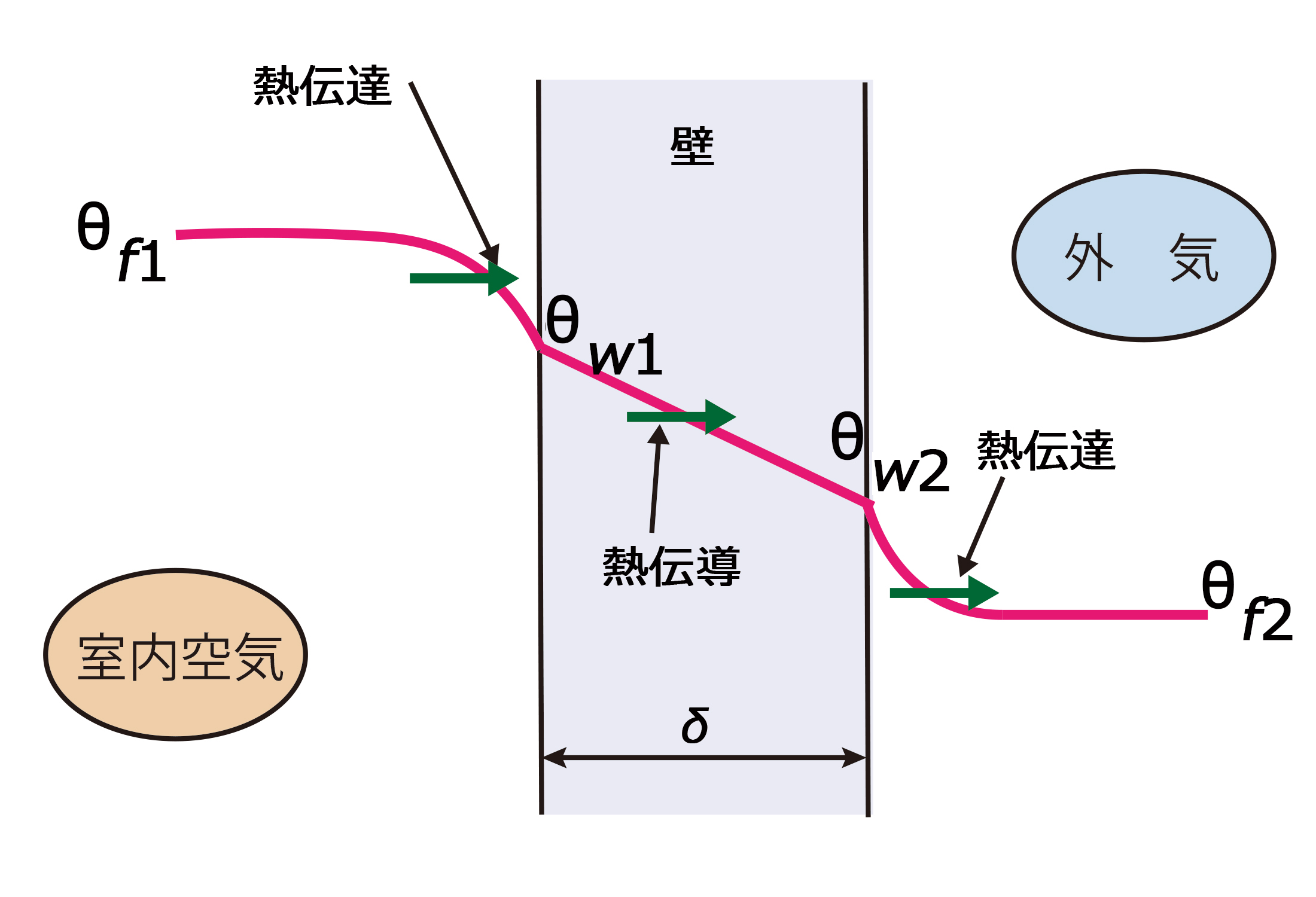
【問題】ローフィンチューブを使用した水冷シェルアンドチューブ凝縮器の仕様および運転条件は下記のとおりである。ただし、冷媒と冷却水との間の温度差は算術平均温度差を用いるものとする。
| 【冷凍サイクルの運転条件】 | |
| 伝熱管の長さ | \(δ\)=1.0 mm |
| 有効内外面積比 | m=3.0 |
| 冷媒側有効伝熱面積 | \(A_{r}\)=3.0 m2 |
| 伝熱管の熱伝導率 | \(λ\)=0.37 kW/(m・K) |
| 冷媒側熱伝達率 | \(α_{r}\)=3.0 kW/(m2・K) |
| 冷却水側熱伝導率 | \(α_{w}\)=9.0 kW/(m2・K) |
| 冷却水量 | \(q_{mw}\)=1.0 kg/sec |
| 冷却水入口温度 | \(t_{w1}\)=30.0 ℃ |
| 冷却水出口温度 | \(t_{w2}\)=36.0 ℃ |
| 冷却水の比熱 | \(c_{w}\)=4.2 kJ/(kg・K) |
1.凝縮負荷\(Φ_{k}\)(kW) は?
2.冷媒と伝熱管外表面の温度差\(ΔT_{r}\)(K)、伝熱管内外表面における温度差\(ΔT_{p}\)(K)、および冷却水と伝熱管内表面の温度差\(ΔT_{w}\)(K)を求め、一般的に伝熱管の熱伝導抵抗が無視できることを簡単に説明せよ。
3. 凝縮負荷が同じ場合、冷却水側の汚れがない場合に比べて、冷却水側の水あかなどの汚れがある場合の凝縮温度の上昇を3K以下としたい。許容される最大の汚れ係数を求めよ。 ただし、伝熱管の熱伝導抵抗は無視できるものとし、汚れ係数\(f\)(m2・K/kW)と凝縮温度以外の条件は変わらないものとする。

この問題の解説は次の「上級冷凍受験テキスト」を参考にしました
まず、問題の概念を図に表すと
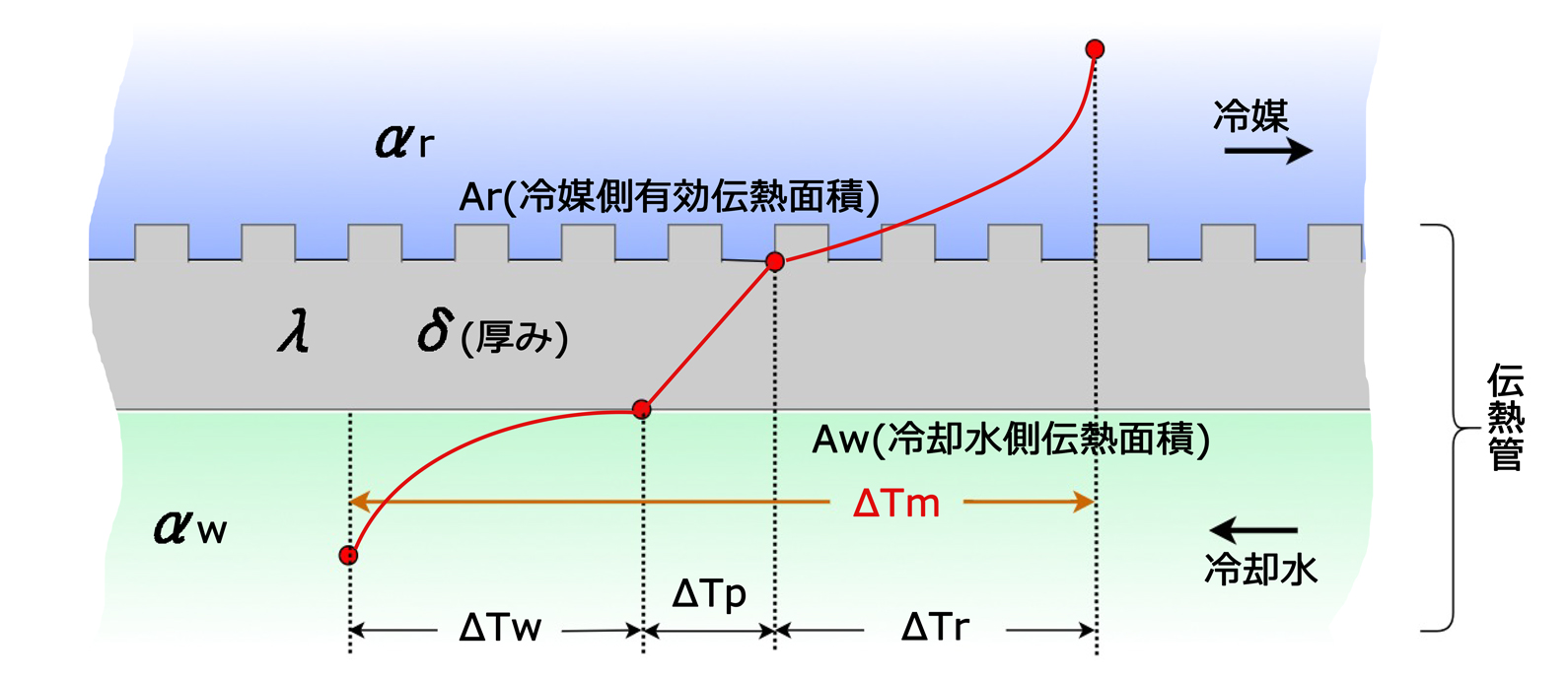
1.凝縮負荷\(Φ_{k}\)(kW) は?
基本式は
2.冷媒と伝熱管外表面の温度差\(ΔT_{r}\)(K)、伝熱管内外表面における温度差\(ΔT_{p}\)(K)、および冷却水と伝熱管内表面の温度差\(ΔT_{w}\)(K)を求め、一般的に伝熱管の熱伝導抵抗が無視できることを簡単に説明せよ。
$$ΔT_{r}=\frac{Φ_{k}}{α_{r}・A_{r}}=\frac{25.2}{3.0×3.0}=2.8 (K)$$
\(Φ_{k}=\frac{λ}{δ}・A_{w}・ΔT_{p}\)より
③冷却水と伝熱管内表面の温度差\(ΔT_{w}\)(K)
\(Φ_{k}=α_{w}・A_{w}・ΔT_{w}\)より
$$ΔT_{w}=\frac{Φ_{k}}{α_{w}・A_{w}}=\frac{Φ_{k}}{α_{w}・\frac{A_{r}}{3}}=\frac{25.2}{9.0×\frac{3.0}{3.0}}=2.8 (K)$$
温度差\(ΔT_{p}\)は\(ΔT_{r}\)及び\(ΔT_{w}\)に比べ無視できるほど小さい
凝縮温度と冷却水温度の算術平均温度差\(ΔT_{m}\)は
水垢が付着し、凝縮温度が最高3K上昇した場合を考えると\(ΔT’_{m}=8.6 (K)\)となる
このときの熱通過率を\(K’\)とすると
また\(K’\)は汚れ係数を考慮すると次のようになる