問題 １
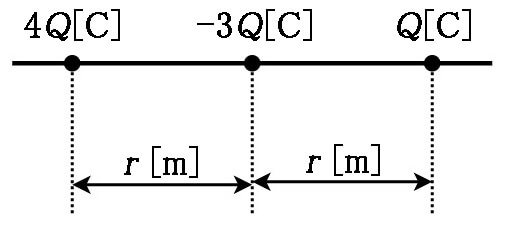
下図のように、真空中に、一直線上に等間隔\(r\)〔m〕で、\(4Q\)〔C〕、\(-3Q\)〔C〕、\(Q\)〔C〕の点電荷があるとき、\(Q\)〔C〕の点電荷に働く静電力\(F\)〔N〕を表す式として、正しいものはどれか。
ただし、真空の誘電率を\(ε_{0}\)〔F／m〕とし、右向きの力を正とする。
| ａ | \(F=\Large{\frac{Q^{2}}{4πε_{0}r^{2}}}\) [N] |
| ｂ | \(F=\Large{-\frac{Q^{2}}{4πε_{0}r^{2}}}\) [N] |
| ｃ | \(F=\Large{\frac{Q^{2}}{2πε_{0}r^{2}}}\) [N] |
| ｄ | \(F=\Large{-\frac{Q^{2}}{2πε_{0}r^{2}}}\) [N] |
解答
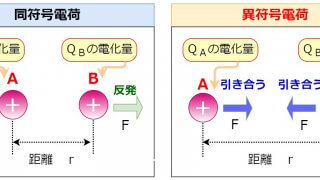
クーロンの法則を用います。クーロンの法則とは、点電荷間に働く反発または引き合う力のことで、それぞれの点電荷の積に比例し、距離の2乗に反比例します。
●\(4Q\)と\(Q\)の間で働くクーロン力を\(F_{0}\)とするとクーロンの法則より（斥力だから右側の正方向に働く）
\(F_{0}=\Large{\frac{1}{4πε_{0}}\frac{4Q^{2}}{4r^{2}}=\frac{1}{4πε_{0}}\frac{Q^{2}}{r^{2}}}\)
●\(-3Q\)と\(Q\)の間で働くクーロン力を\(F_{1}\)とするとクーロンの法則より（引力だから左側の負方向に働く）
\(F_{1}=\Large{-\frac{1}{4πε_{0}}\frac{3Q^{2}}{r^{2}}}\)
点電荷\(Q\)に働く力\(F\)は
\(F=F_{0}+F_{1}=\Large{-\frac{Q^{2}}{2πε_{0}r^{2}}}\)
問題 ２
下図のように、円形コイルに磁束を加えるときの起電力に関する記述として、不適当なものはどれか
| ａ |
円形コイルと鎖交しない磁束は、起電力の発生に関与しない
|
| ｂ | 磁束が増加したとき、アの方向に電流を流す起電力が発生する |
| ｃ |
円形コイルの巻数を増やすと、起電力は大きくなる
|
| ｄ | 加えている磁束を時間に正比例して増加させると、起電力も増加する |
解答
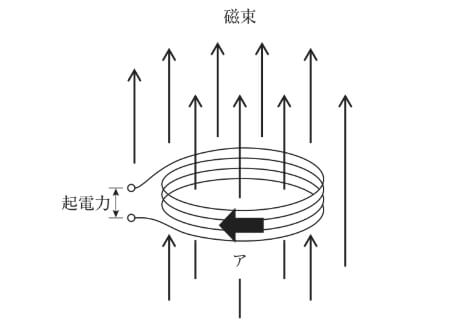
ａ‥円形コイルと鎖交しない磁束（コイルの外側のある磁束）は、起電力の発生に関与しない。［正しい］
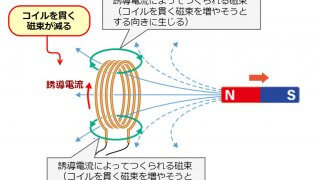
ｂ‥レンツの法則より下向きの磁束が発生するような電流の向きを考えれば、右ねじの法則によりアの方向に電流を流すように起電力が発生する。［正しい］
ｃ‥ファラデーの電磁誘導の法則よりコイルの巻数を増やすと発生する誘導起電力が大きくなります。また、磁石を速く動かしたり、磁石の磁力が強いときも起電力は大きくなります。［正しい］
ｄ‥.磁束が時間に比例して増加しているということは、磁束の変化の割合は一定なので、ファラデーの電磁誘導の法則より起電力も一定になります。［間違い］
