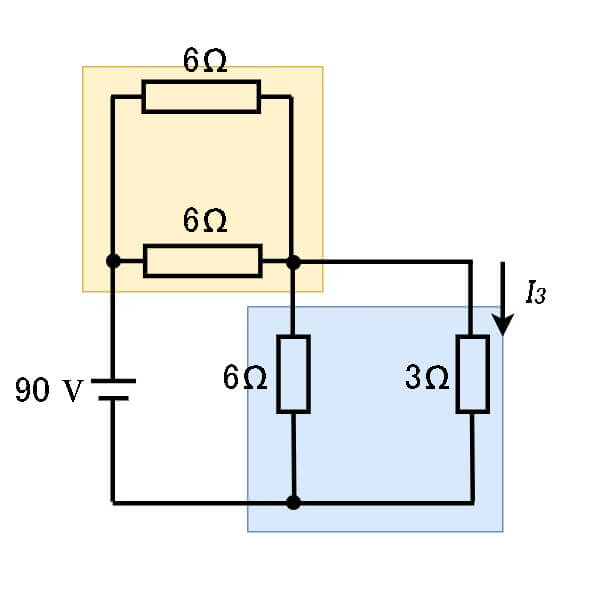
問題 2
1.まず回路全体の電流の大きさを求めます。
1-1 上図のオレンジ2つの並列抵抗( 6Ω、6Ωの部分)の合成抵抗\(R_{1}\)は
\(\frac{1}{R_{1}}=\frac{1}{6}+\frac{1}{6}=\frac{1}{3}\)
\(R_{1}=3\)
1-1 上図のオレンジ2つの並列抵抗( 6Ω、6Ωの部分)の合成抵抗\(R_{1}\)は
\(\frac{1}{R_{1}}=\frac{1}{6}+\frac{1}{6}=\frac{1}{3}\)
\(R_{1}=3\)
1-2 上図の水色の2つの並列抵抗(6Ω、3Ωの部分)の合成抵抗\(R_{2}\)は
\(\frac{1}{R_{2}}=\frac{1}{6}+\frac{1}{3}=\frac{1}{2}\)
\(R_{2}=2\)
1-3. 回路全体の合成抵抗は、
3(Ω)+2(Ω)=5(Ω)
\(\frac{1}{R_{2}}=\frac{1}{6}+\frac{1}{3}=\frac{1}{2}\)
\(R_{2}=2\)
1-3. 回路全体の合成抵抗は、
3(Ω)+2(Ω)=5(Ω)
2.全体を流れる電流はオームの法則から
90(V)/5(Ω)=18(A)
90(V)/5(Ω)=18(A)
3.\(I_{3}\)は、2抵抗の分流の比の計算。
\(I_{3}=18×\frac{6}{(3+6)}=12(A)\)
\(I_{3}=18×\frac{6}{(3+6)}=12(A)\)